1. Определение комплексного числа.
Комплексным числом называется выражение вида х+іу, где х и у - действительные числа, а і- символ, который называется мнимой единицей, числа х и у называется, соответственно, действительной и мнимой частям комплексного числа х+іу и обозначаются символами
х= Re (x+iy), y= Im (x+iy). (23.1)
Если в частности, у=0, то х+і0 читается совпадающим с действительным числом х; если х=0, то 0+іу обозначается просто іу и называется чисто мнимым.
Таким образом, в состав комплексных чисел входят также действительные числа. Если множество всех комплексных чисел обозначают через C, то R 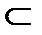 C.
C.
Определим на множестве комплексных чисел понятия равенства и простейшие операции.
· Два комплексных числа считаются равными, если равны порознь их действительные и мнимые части, то есть
х1 +іу1 =х2+іу2
Считаются равными тогда и только тогда, когда х1=х2, у1=у2.
· Комплексное число х-іу называется сопряженными с комплексным числом z=х+iy и обозначается
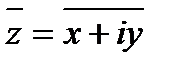 =х -іу (23.2)
=х -іу (23.2)
Комплексное число х+iy принято обозначать одной буквой Z, т.е. Z=х+iy, тогда формула (23.1) пишется в виде:
Х= Re(x+iy)= ReZ, Y= Im(х+iy)=Im  а из (23.2)
а из (23.2) 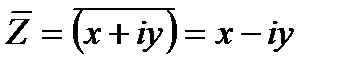 (23.3)
(23.3)
(Re и Im –являются сокращениями французских слов Reel - действительный и Imaginanize - мнимый).
Число 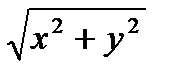 называется модулем комплексного числа Z=х+iy и обозначается
называется модулем комплексного числа Z=х+iy и обозначается 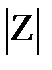 :
:
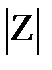 =
= 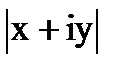 =
= 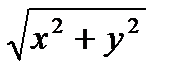 (23.4)
(23.4)
Очевидно, 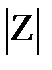
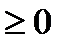 , причем
, причем 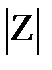 =0, тогда и только тогда, когда
=0, тогда и только тогда, когда 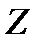 =0. Модуль действительного числа совпадает с абсолютной величиной этого числа.Отметим две формулы:
=0. Модуль действительного числа совпадает с абсолютной величиной этого числа.Отметим две формулы:
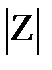 =
= 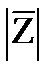 (23..5)
(23..5)
Z 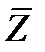 =
= 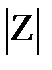
 (23.6)
(23.6)
которые вытекают из (23.3), (23.4) и равенства
ZZ =(х+iy)(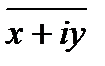 )= x2+y2
)= x2+y2
Теперь рассмотрим операции над комплексными числами.
I. Сложение. Суммой Z1+ Z2 комплексных чисел Z1=х1+iy1 и Z2-=х2+iy2
называется комплексное число
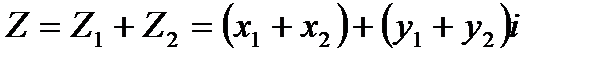 (23.7)
(23.7)
Из этого определения непосредственно вытекают следующие законы сложения:
А) переместительный: (или закон коммутативности)
Z1+Z2=Z2+Z1,
Б) сочетательный (ассоциативности):
Z1 + (Z2+Z3) = (Z1+Z2) + Z3.
Если Z1 и Z2 действительные числа (т.е. У1=У2=0), то определение (23.7) совпадает с определением сложения для действительных чисел.
Сложение допускает обратную операцию: для любых комплексных чисел Z1=х1+ iy1 и Z2= х2+ iy2 можно найти такое число Z, что Z2+Z=Z1. Это число называется разностью чисел Z1 и Z2 и обозначается символом Z1- Z2.
Очевидно
Z= Z1- Z2 = (х1-х2) +і (у1-у2) (23.8)
Умножение. Произведением Z1,Z2 комплексных чисел Z1=х1+iy1 и Z2=х2+iy2 называется комплексным число
Z= Z1* Z2 = (Х1Х2-У1У2) + і(Х1У2+У1Х2) (23.9)
Умножение комплексных чисел обладает следуюшими своиствами:
А) переместительный: Z1* Z2= Z2* Z1:
Б) сочетательный: Z1 (Z2 *Z3) = (Z1* Z2) Z3:
В) распределительный (дистрибутивности)
Z1 (Z2 +Z3) = Z1 Z2+ Z1 Z3
Если Z1 и Z2 – действительные числа, то определение (23.9) совпадает с обычным. При Z1= Z2=і из определения произведения следует:
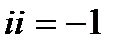 (23.10)
(23.10)
Умножение также допускает обратную операцию, если только данный множитель не равен нулю. Пусть Z2 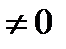 , тогда можно найти такое число Z, что Z2 Z= Z1 , для этого, согласно (23.9) надо решить систему уравнений
, тогда можно найти такое число Z, что Z2 Z= Z1 , для этого, согласно (23.9) надо решить систему уравнений
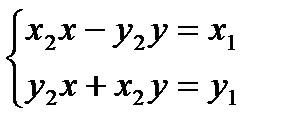 (23.11)
(23.11)
которая при Z2 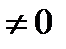 всегда однозначно разрешима, так как ее определитель Х
всегда однозначно разрешима, так как ее определитель Х 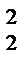 +У
+У 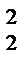 > 0. Это число называется частным двух чисел Z1 и Z2 и обозначается символом Z.
> 0. Это число называется частным двух чисел Z1 и Z2 и обозначается символом Z.
Решая систему (23.11)
Z = Z1 /Z2 = 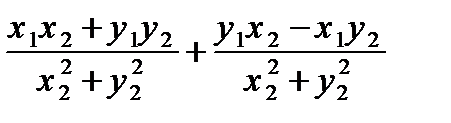 i (23.12)
i (23.12)
легко заметить, что (23.12) может быть получено умножением числителя и знаменателя дроби Z1/Z2 на 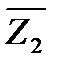 .
.
Пример 23.1. Даны числа Z1=1+2i, Z2 =4+3i найти Z1Z2 и 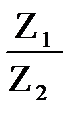
Решение. Согласно формуле (23.9) имеем
Z1Z2= (1+2i) (4+3i) ==(1*4-2*3)+i(1*3+2*4)=2+11i.
Применяя формулу (1.12), получим
Z= 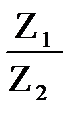 = =
= = 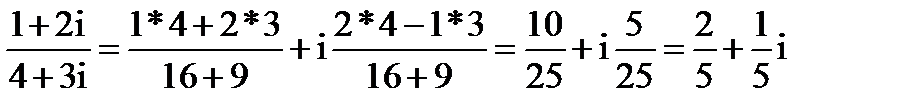 .
.
3. Возведение в целую степень. Произведение n равных чисел Z называется n -й степенью числа Z и обозначается символом Zn:
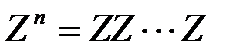 (23.13)
(23.13)
n –раз.
Обратная операция – извлечение корня – определяется следующим образом: число W называется корням n-й степени из числа Z,если Wn=Z (обозначается символом 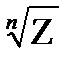 , причем для n=2 пишут просто
, причем для n=2 пишут просто  ). Эта для всякого Z
). Эта для всякого Z 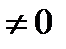 корень
корень 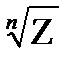 имеет n различных значений.
имеет n различных значений.
Так как ii=i2=-1 мы можем писать
i= 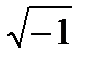 (23.14)
(23.14)
2. Геометрическая иллюстрация
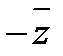
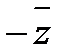
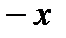
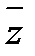
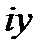
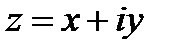
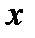
| Рис 1.1 |
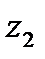
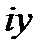
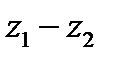
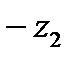
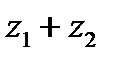
| Рис 1.2 |
Такое соответствие между комплексными числами и точками плоскости, очевидно, является взаимно однозначным. При этом действительные числа изображаются точками оси абсцисс, а число мнимые точками оси ординат. Поэтому ось абсцисс называется действительной осью, а ось ординат - мнимой осью. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Комплексное число Z изображается также вектором с началом точке 0 и концом в точке Z. Рис 1.1 Из формулы (1.4) и (рис. 1.1) и видно, что длина вектора Z равна 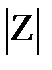 и имеют место неравенства.
и имеют место неравенства.
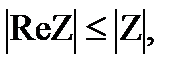
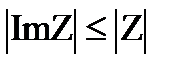
С помощью векторной интерпретации наглядно иллюстрируются сложение и вычитание комплексных чисел. Из формулы (23.7) вытекает, что число по обычному правилу сложения векторов Z1 Z2(рис.1.2.).Вектор Z1-Z2 строится как сумма векторов Z1и -Z2. (рис.1.2.)
Из (рис.1.2) видно, что расстояние между точками Z1 и Z2 равно длине вектора Z1-Z2, то есть равно 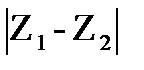
Пример 23.2. Множество точек Z, удовлетворяющих уравнению 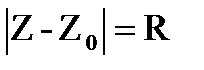 , есть окружность радиуса R с центром в точке
, есть окружность радиуса R с центром в точке  , так
, так  - расстояние между точками Z и Z0.
- расстояние между точками Z и Z0.
Пример 23.3. МножествоZ, удовлетворяющих уравнению 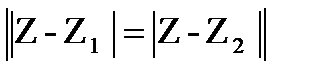 , есть множество точек равноудаленных от точек Z1и Z2 . Следовательно, это уравнение прямой, перпендикулярной отрезку, соединяющему точки Z1 и Z2, и проведенной через его середину.
, есть множество точек равноудаленных от точек Z1и Z2 . Следовательно, это уравнение прямой, перпендикулярной отрезку, соединяющему точки Z1 и Z2, и проведенной через его середину.
Пример 23.4. а) Множество точек Z удовлетворяющих уравнению  ,
,  есть эллипс с фокусами в точках Z1,Z2 и с большой полуосью, равной а так как
есть эллипс с фокусами в точках Z1,Z2 и с большой полуосью, равной а так как  - сумма расстояний от точки Z до точек Z1 иZ2 .
- сумма расстояний от точки Z до точек Z1 иZ2 .
б) Аналогично, уравнение 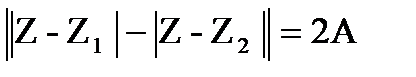 , где
, где 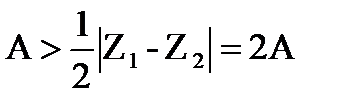 , является уравнением гиперболы с фокусами в точках Z1,Z2 и с действительной полуосью, равной а.
, является уравнением гиперболы с фокусами в точках Z1,Z2 и с действительной полуосью, равной а.
Неравенства треугольника. Для любых комплексных чисел Z1 и Z2 имеют место неравенства
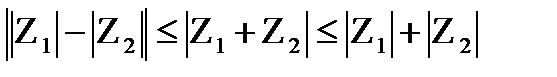 (23.15).
(23.15).
Доказательство. Длина сторон треугольника с вершинами в точках 0, Z1 , Z1 + Z2 равны  и
и 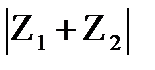 (рис.1.2). Следовательно, неравенство (23.15) является известным из элементарной геометрии неравенством для длин сторон треугольника.
(рис.1.2). Следовательно, неравенство (23.15) является известным из элементарной геометрии неравенством для длин сторон треугольника.
Следствие. Для любых комплексных чисел Z1 , Z2 ,… Zn имеет место неравенство
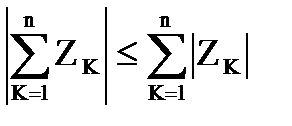 (23.16)
(23.16)
§3.Тригонометрическая алгебраическая, показательная формы записи комплексных чисел. Аргумент и главное значение аргумента. Форму записи комплексного числа Z в виде Z= х+iу называет алгебраической.
| Z=х + iy алгебраическая форма комплекс- ного числа. |
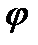
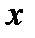
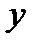
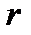
| Рис23.3 |
комплексной плоскости однозначно определяется не только декартовыми координатами Х, У, но и полярными координатами 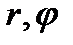 (рис.23.3), где r =
(рис.23.3), где r = 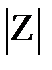 - расстояние от точки до точки Z, а
- расстояние от точки до точки Z, а  - угол между действительной осью и вектором Z, отсчитываемый от положительного направления действительной оси. При этом если отсчет ведется против часовой стрелки, то величина угла считается положительной, а если по часовой стрелке - отрицательной.
- угол между действительной осью и вектором Z, отсчитываемый от положительного направления действительной оси. При этом если отсчет ведется против часовой стрелки, то величина угла считается положительной, а если по часовой стрелке - отрицательной.
Этот угол называется аргументом комплексного числа Z (Z 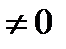 ) и обозначается так:
) и обозначается так:  =arg Z (обозначение arg является сокращением французского слова argument (аргумент)). Для числа Z =0 аргумент не определяется, поэтому во всех дальнейших рассуждениях, связанных с понятием аргумента предполагается, что Z
=arg Z (обозначение arg является сокращением французского слова argument (аргумент)). Для числа Z =0 аргумент не определяется, поэтому во всех дальнейших рассуждениях, связанных с понятием аргумента предполагается, что Z 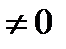
Из рис 23.3. видно, что
x = cos  , y = rsin
, y = rsin  (23.17)
(23.17)
Следовательно, любое комплексное число Z 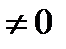 можно представить в виде.
можно представить в виде.
Z=r (cos  +isin
+isin  ) (23.18)
) (23.18)
Запись комплексного числа в виде (23.18) называется тригонометрической формой комплексного числа. Таким образом запись Z=r (cosφ+isinφ) тригонометрическая форма комплексного числа. Из формулы (23.17) вытекает, что если
z=х+iу,  =argz, то cos
=argz, то cos  =
= 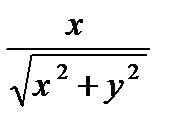 , sin
, sin  =
= 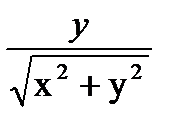 (23.19)
(23.19)
Система (23.19) имеет бесконечно много решений, и все эти решения задаются формулой
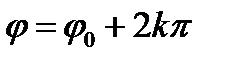 ,
, 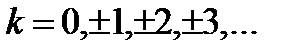
Таким образом, аргумент комплексного числа определяется неоднозначно: если 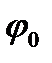 - одно из значений аргумента комплексного числа Z, то все значения аргумента этого числа находится по формуле
- одно из значений аргумента комплексного числа Z, то все значения аргумента этого числа находится по формуле
arg Z= 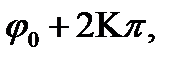
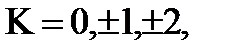 … (23.20)
… (23.20)
Из системы (23.19) видно, что аргумент  комплексного числа Z= х+iу удовлетворяет уравнению
комплексного числа Z= х+iу удовлетворяет уравнению
tg 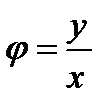 (23.21)
(23.21)
Следует иметь в виду, что не все решения уравнения (23.21) являются решениями системы (23.19)
Таким образом, либо 0 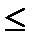 arg Z
arg Z 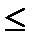
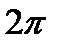 , либо -
, либо -  .
.
Значение arg Z = arg (x+iy) легко выразить через arсtg 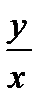 . Учитывая что-
. Учитывая что- 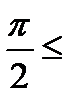 arctg
arctg 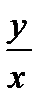
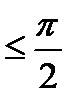 в случае, если 0
в случае, если 0 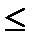 arg Z<
arg Z< 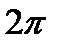 получаем
получаем
если  если если 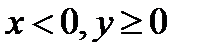 если если  если если 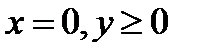 если если 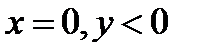 |
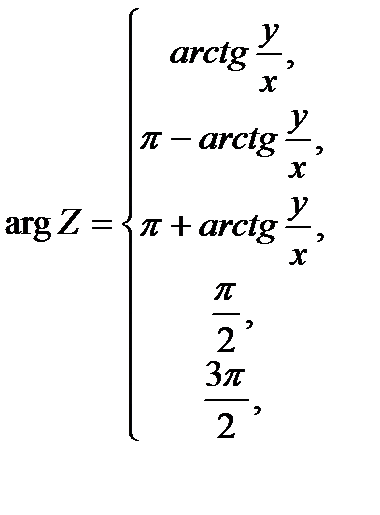
Если же - 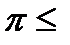 arсtg
arсtg 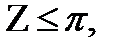 то
то
если  если если 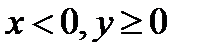 если если 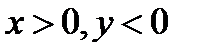 если если 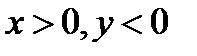 если если 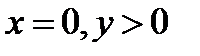 если если  |
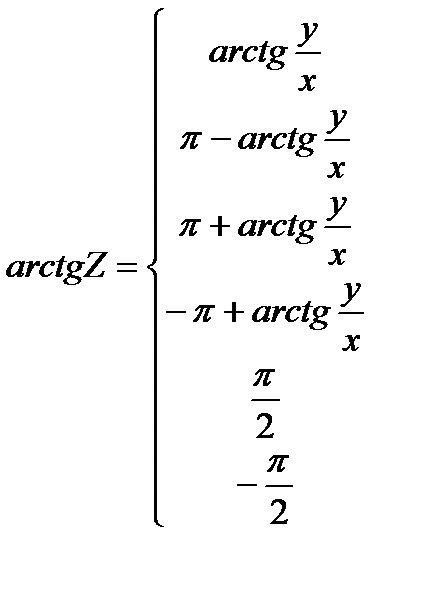
В дальнейшем, если не оговорено особо будем считать, что - 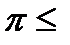 arg Z
arg Z 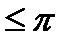
Пример 23.5. Даны числа Z1=-3+4i, Z2 =4-3i. Найдите главные значения аргумента этих чисел. Запишите эти числа в тригонометрической форме.
Решение.
Так как ReZ1=x=-3, ImZ1=y=4, то arg Z= 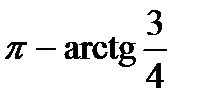 , ReZ2=x=4, ImZ2=y= -3
, ReZ2=x=4, ImZ2=y= -3
Поэтому arg Z2=  , поскольку
, поскольку
r= 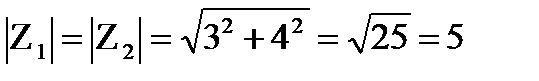
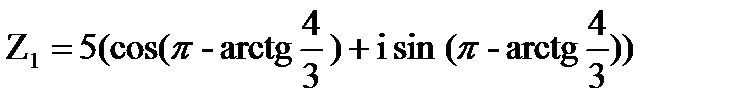
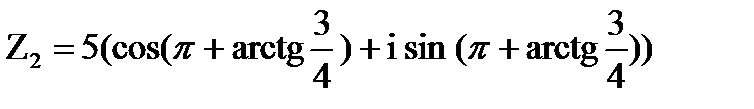
Пример 23.6. Найдем аргумент комплексного числа Z=-1-i.
Так как точка Z=-1-i. лежит в третьей четверти и tg 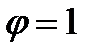 , то
, то
arg (-1- i) =  ,
,  ...
...
Если  =1,
=1,  =arg
=arg 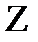 , то по формуле (23..18) имеем z=cos
, то по формуле (23..18) имеем z=cos  +isin
+isin  . Комплексное число cos
. Комплексное число cos  +isin
+isin  обозначается символом еi
обозначается символом еi 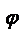 , т.е. функция еi
, т.е. функция еi 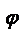 для любого действительного числа
для любого действительного числа  определяется формулой Эйлера
определяется формулой Эйлера
е i 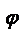 = cos
= cos  +isin
+isin  (23.22)
(23.22)
В частности 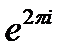 =1 е
=1 е 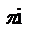 =-1,
=-1, 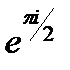 =i,
=i, 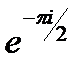 =- i,
=- i, 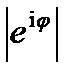 =1 для любого действительного числа
=1 для любого действительного числа 
Из (23.22) заменой φ на – φ получим
е-iφ=cos φ-і sin φ (23.23)
Сложением и вычитанием равенств (23.22) и (23.23) получаем формулы Эйлера
cos  =
= 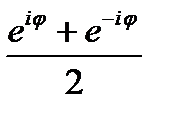 sin
sin  =
= 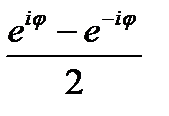 (23.24)
(23.24) 
с помощью которых тригонометрические функции выражаются через показательную функцию.
Функция еi  обладает обычными свойствами показательной функции, как если бы число i было действительным. Отметим основные из них:
обладает обычными свойствами показательной функции, как если бы число i было действительным. Отметим основные из них:
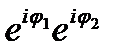 =
= 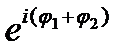 (23.25)
(23.25)
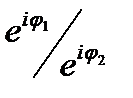 =
= 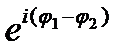 (23.26)
(23.26)
(еi 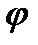 )n = еin
)n = еin  , n=0,
, n=0, 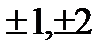 ... (23.27)
... (23.27)
Докажем равенство (23.25).Имеем
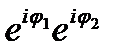 =
= 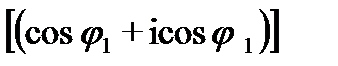
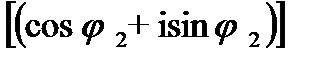 =
= 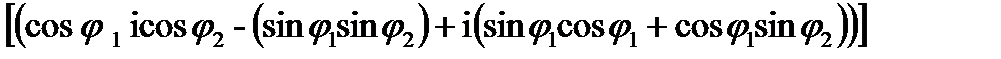
= cos 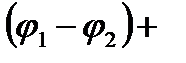 i sin
i sin 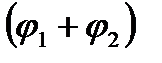 =е i
=е i 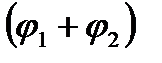
аналогично проверяется равенство (23.26). Равенство (23.27) получается из (23.25) и (23.26).
Из (23.27) и (23.22) вытекает формула Муавра
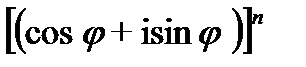 =cosn
=cosn  +i sinn
+i sinn  ,n=0
,n=0 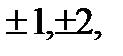 (23.28)
(23.28)
Из формулы (23.18) и (23.22) следует, что любое комплексное число 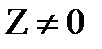 можно представить в виде
можно представить в виде
Z= rei  (23.29) где r =
(23.29) где r = 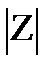
 =arg
=arg 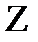 . Запись комплексного числа в виде (23.29) называется показательной формой комплексного числа. С помощью (23.25) и (23.26) можно получить формулы умножения и деления комплексных чисел, записанных в показательной форме:
. Запись комплексного числа в виде (23.29) называется показательной формой комплексного числа. С помощью (23.25) и (23.26) можно получить формулы умножения и деления комплексных чисел, записанных в показательной форме:
Z 1 Z 2 = r1 еi 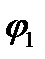 . r2 еi
. r2 еi 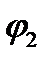 = r1 r2 еi
= r1 r2 еi 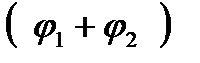 (23..30)
(23..30)
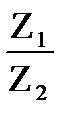 = r1 еi
= r1 еi 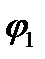 / r2 еi
/ r2 еi 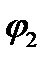 = r1/ r2 е i
= r1/ r2 е i 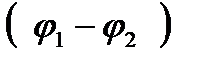 (23.31)
(23.31)
Из формулы (23.30) следует, что модуль произведения двух комплексных чисел равен произведению модулей этих чисел:
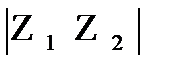 =
= 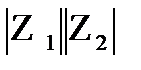 а сумма аргументов сомножителей является аргументом произведения: если
а сумма аргументов сомножителей является аргументом произведения: если
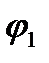 =argZ1,
=argZ1, 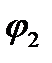 =argZ2 тo
=argZ2 тo 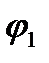 +
+ 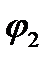 =arg(Z1Z2 ) (23.32)
=arg(Z1Z2 ) (23.32)
Аналогично из формулы (23.31) вытекает, что модуль частного двух комплексных чисел равен частному модулей этих чисел:
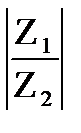 =
= 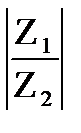 , Z2
, Z2 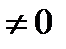 , а разность аргументов делимого и делителя является аргументом частного, если
, а разность аргументов делимого и делителя является аргументом частного, если 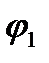 =arg Z1 ,
=arg Z1 , 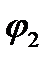 =arg Z2 ,то
=arg Z2 ,то 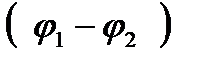 = arg
= arg 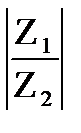 (23.33)
(23.33)
Таким образом, при умножении и делении комплексных чисел, записанных в тригонометрической форме, имеет место следующая теорема.
 2015-03-07
2015-03-07 13764
13764
