При умножении двух комплексных чисел их модули умножаются, а аргумент складывается. При делении комплексных чисел их модули делятся, а аргумент вычитывается.
Доказательство. Пусть
Z 1 = r1 (cos 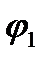 + isin
+ isin 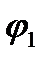 ).Z 2 = r 2 (cos
).Z 2 = r 2 (cos 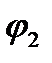 + isin
+ isin 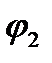 )
)
тогда
Z1Z2=r1r2 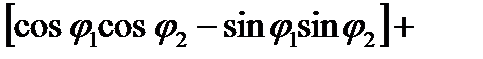
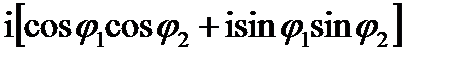 =
=
= r1r2 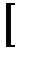 cos
cos 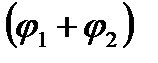 +i sin
+i sin 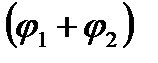
Аналогично, легко получить, что
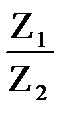 =
= 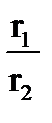
 cos
cos 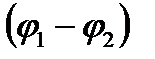 +i sin
+i sin 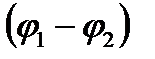
 r 2
r 2 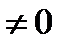
из доказанной теоремы следует правило возведения комплексного числа в целую положительную степень
Z n= 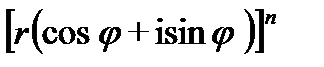 =
= 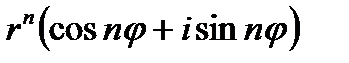
Очевидно i4m=1, i4m+1=i, i4m+2=-1, i4m+3=-i m>0 любое целое число.
Пример 23.7. Число i82+3i27/ i44-2i51 записать в алгебраической форме
Решение. Так как i82=i4*20+2=-1, i37=i4*9+1= i
i44= (i4)11=1 i51=i4*12+3= -i, то Z = (-1+3i) /
/ (1+2i)
поэтому
Z= 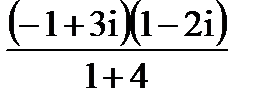 =
= 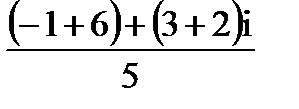 =
= 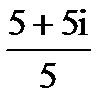 =
= 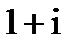
 2015-03-07
2015-03-07 1066
1066








