(1-i 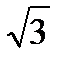 )3 (1+i)2 =(
)3 (1+i)2 =(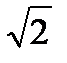 е
е 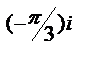 )3 (
)3 (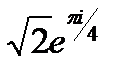 )2=
)2=
=23 e 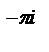 2e
2e 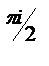 =23(-1)2i=-16i
=23(-1)2i=-16i
Отметим, что из геометрической интерпретации (рис23.3) вытекает правило равенства комплексных чисел, записанных в показательной форме: если Z 1 = r1 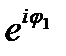 Z2=r2
Z2=r2 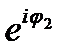 то равенство Z 1 =Z 2 имеет место тогда и только тогда, когда r 1 = r 2 и
то равенство Z 1 =Z 2 имеет место тогда и только тогда, когда r 1 = r 2 и 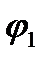 =
= 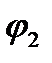 +2k
+2k 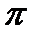 где k- некоторое целое число. Таким образом, Z 1 =Z 2 тогда и только тогда, когда
где k- некоторое целое число. Таким образом, Z 1 =Z 2 тогда и только тогда, когда
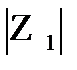 =
= 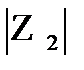 и arg Z1=arg Z2+2
и arg Z1=arg Z2+2 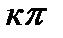 (23..34)
(23..34)
где к – целое число.
С помощью комплексных чисел удобно записать многие формулы аналитической геометрии.
Пусть А1=(х1 ,у1) А2=(х2 ,у2) 0=(0,0) - точки на плоскости (х, у) 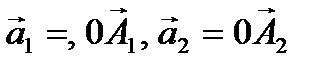 векторы. Этим векторам отвечают комплексные числа Z1=х1+iy1, Z2 =х2+iy2 Имеем:
векторы. Этим векторам отвечают комплексные числа Z1=х1+iy1, Z2 =х2+iy2 Имеем:
Z 1Z 2 = х1 у1 +х2 у2+i (х1 у2-х2 у1)
Действительная часть этого выражения равна скалярному произведению векторов
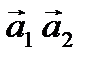 : (а1 а2) = Re(Z 1Z 2),
: (а1 а2) = Re(Z 1Z 2),
а его мнимая часть равна ориентированной площади S треугольника с вершинами в точках О, А1, А2
S= Im (Z 1Z 2)= 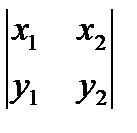
Пусть А(х, у) – точка плоскости (х, у) найдем ее координаты (х, у) в новой системе координат, полученной из старой поворотом на угол 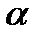 Точке А отвечает комплексное число х + iy=re i
Точке А отвечает комплексное число х + iy=re i  Тогда
Тогда
х1+iy1=rei(φ-α)=reiφ e-iα=(x+iy)e-iα,то есть
х1+iу1= (х +iу)(cos  -isin
-isin  )
)
Отсюда, приравнивая действительные и мнимые части, находим
Х1=х cos  +у sin
+у sin  ,у1=-х sin
,у1=-х sin  +у cos
+у cos 
Пример 23.9. Записать в тригонометрической форме комплексное число Z=-1-i 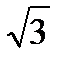
Решение. Так как любое комплексное число Z=х+iу (Z¹0) можно записать в тригонометрической форме
Z =r (cos j+ i sin j), где r= 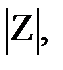
 = arg Z
= arg Z
Имеем 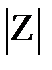 =
= 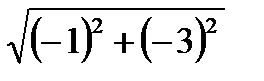 =2
=2
tg  =
= 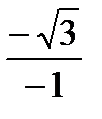 =
= 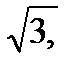
 =
= 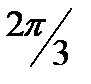
Следовательно,
-1-i 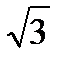 =2
=2 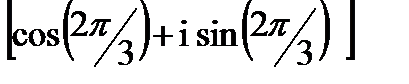
Пример 23.10. Найти действительные корни уравнения cosх +i sinх= 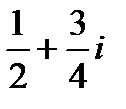
Решение. Данное уравнение корней не имеет. В самом деле, это уравнение равносильно следующим:
Cos х = 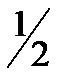 sin х =
sin х = 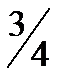
Последние уравнения несовместны, так как
cos2х + sin2х= 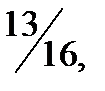 что невозможно ни при каких значениях х.
что невозможно ни при каких значениях х.
Пример 23.11. Найти все комплексные числа Z 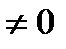 , удовлетворяющие условию Zn-1=
, удовлетворяющие условию Zn-1= 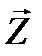
Решение. Так как любое число можно записать в показательной форме Z=rеiφ
r= 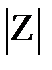 ,
,  = arg Z. Пусть Z=rеiφ. Тогда
= arg Z. Пусть Z=rеiφ. Тогда 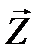 =rе-iφ согласно условию rn-1ei(n-1)j= rе-iφ
=rе-iφ согласно условию rn-1ei(n-1)j= rе-iφ
или rn-2einφ=1.Откуда rn-2=1 т.е. r=1 и in  =2
=2 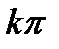 i, т.е.
i, т.е.
 =
= 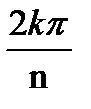 где k=0,1,2…..n-1, следовательно, Z k = е
где k=0,1,2…..n-1, следовательно, Z k = е 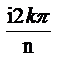 (k=0,1,2,… n-1).
(k=0,1,2,… n-1).
Пример 23.12. Вычислить (-1+i 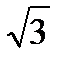 )60
)60
Решение. Пользуясь формулой Муавра, представим число Z =(-1+i 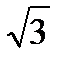 )60 в тригонометрической форме
)60 в тригонометрической форме
(-1+i 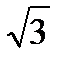 )60=260
)60=260 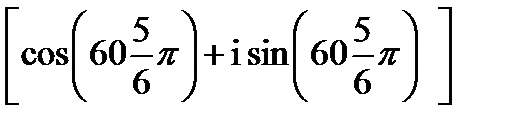 =
=
=260(cos 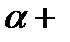 isin 50
isin 50 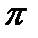 )=260
)=260
Пример 23.13. Доказать, что многочлен
f(x)= (cos  +x sin
+x sin  )n- cosn
)n- cosn  - x sinn
- x sinn  делится на х2+1
делится на х2+1
Решим. Имеем х2+1= (х + i)(х - i). По формуле Муавра
f(i)= (cos  +i sin
+i sin  )n- cosn
)n- cosn  - i sinn
- i sinn  = =cosn
= =cosn  +i sinn
+i sinn  - cosn
- cosn  - i sinn
- i sinn  =0.
=0.
Аналогично f(-1)=0. Значит f(x) делится на х2+1
§ 4. Извлечение корня из комплексного числа.
Операция извлечения корня целой положительной степени из комплексного числа определяется как операция, обратная возведению в целую положительную степень.
Число 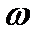 называется корнем n – й степени (n
называется корнем n – й степени (n 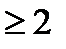 ) из числа z, если
) из числа z, если 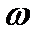 n=z. Обозначим
n=z. Обозначим 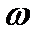 =
= 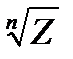 =z
=z 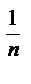
Пусть z=r (cos  +isin
+isin  ), r>0,
), r>0,
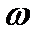 =
= 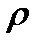 (cos
(cos 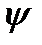 +isin
+isin 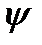 ), тогда по определению и теоремы 1.1
), тогда по определению и теоремы 1.1
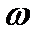 n=
n= 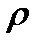 n(cos
n(cos 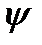 +isin
+isin 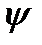 )=r(
)=r(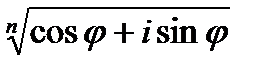 ) отсюда
) отсюда 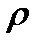 n=r, n
n=r, n 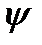 =
=  +
+ 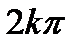 . Следовательно
. Следовательно
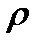 =
= 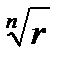
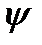 =
= 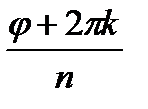 , k=0,1,2,…n-1. Здесь
, k=0,1,2,…n-1. Здесь 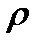 = n
= n 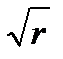 ,
, 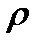 >0 арифметическое значение корня из положительного вещественного числа. Таким образом, если мы берем число
>0 арифметическое значение корня из положительного вещественного числа. Таким образом, если мы берем число 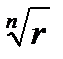 (cos
(cos 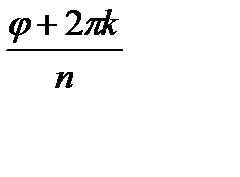 +isin
+isin 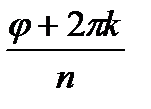 ), то при любом целом k положительном или отрицательном n -я степень этого числа равна
), то при любом целом k положительном или отрицательном n -я степень этого числа равна  . Таким образом,
. Таким образом,
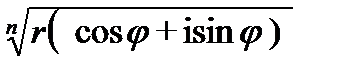 =
= 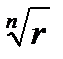 (cos
(cos 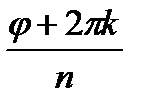 +isin
+isin 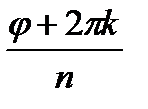 )
)
Пример 23.14. Найти все значения 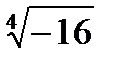
Решение. Так как arg(-16)= 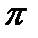
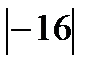 =16, то -16=16(сos
=16, то -16=16(сos 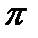 +isin
+isin 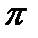 )
) 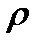 =
= 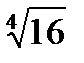 =2
=2 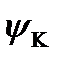 =
= 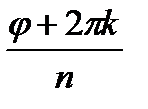 k =0,1,2,3 следовательно
k =0,1,2,3 следовательно
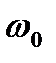 =2(cos
=2(cos 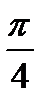 +isin
+isin 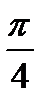 ) =
) = 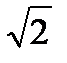 (1+i)
(1+i)
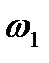 =2(cos
=2(cos 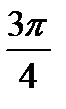 +isin
+isin 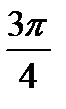 ) =
) = 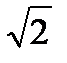 (-1+i)
(-1+i)
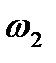 =2(cos
=2(cos 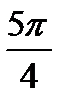 +isin
+isin 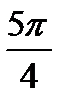 ) =
) = 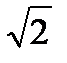 (-1-i)
(-1-i)
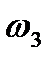 =2(cos
=2(cos 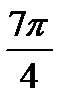 +isin
+isin 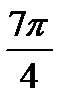 ) =
) = 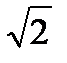 (1-i)
(1-i)
Так как 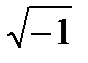 =1 (cos
=1 (cos 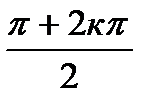 +isin
+isin 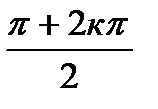 ) к=0,1, то
) к=0,1, то 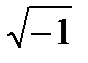 имеет два значения i и – i.
имеет два значения i и – i.
Таким образом, число i одно из значений 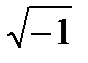
 2015-03-07
2015-03-07 977
977








