Теорема24.2

Из сходимости последовательности

{Z_n}={x_n+iy_n}={r_n(cosj_n+isinj_n)}

к числу

Z₀=х₀+iy₀= {r₀(cosj₀+isinj₀)}

при соответствующем выборе аргументов j₀ и j_n следует, что

, .

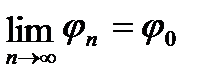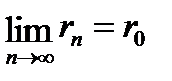Справедливость утверждения следует из теоремы 24.1. о непрерывности функци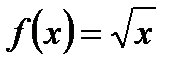и

и ,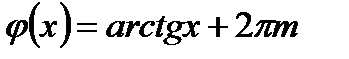

так как

,

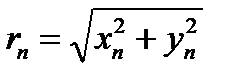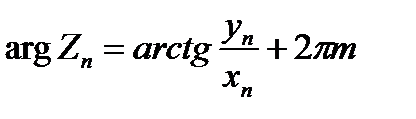
Теорема 24.3. (Критерий Коши).

Для того чтобы последовательность {Z_n} сходилась, необходимо и достаточно, чтобы для любого e>0 существовало число N(e) такое, что при любых n> N и любом р=1,2,... выполнялось неравенство

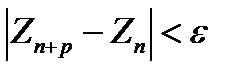
Рассмотрим последовательность 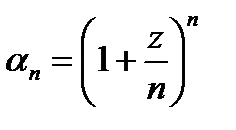, где Z=х+iy любое конечное комплексное число. Чтобы доказать существование и найти 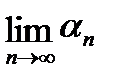, рассмотрим 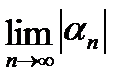и .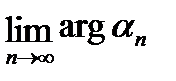

Находим

=

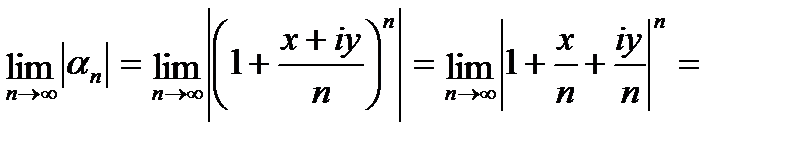
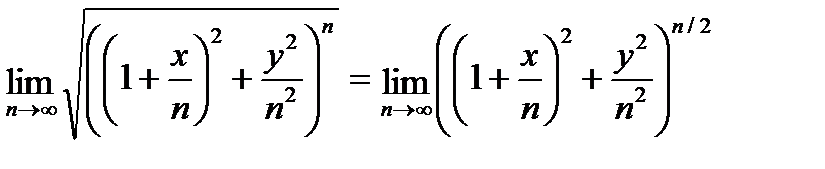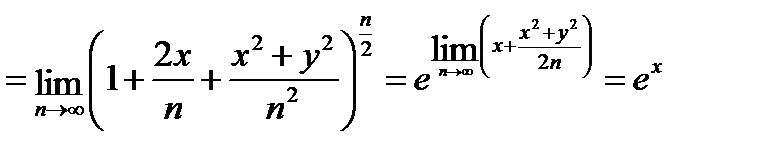
Так как при возведении в целую положительную степень комплексного числа его аргумент умножается на эту степень, то

,

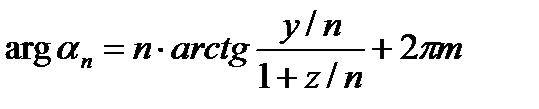где m – любое целое число.

Поэтому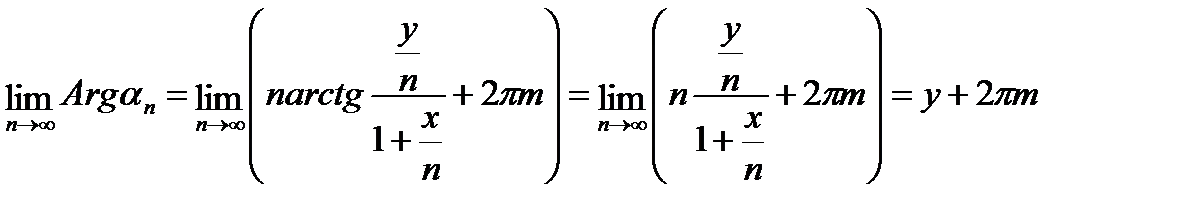

.

Согласно теоремы 2.2. имеем

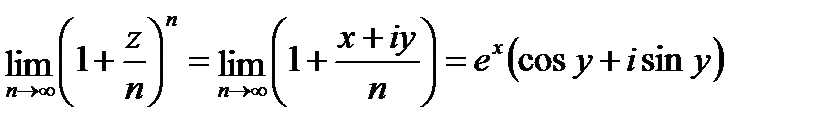
По определению положим

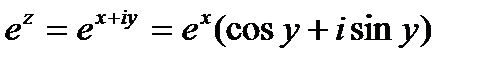(24.1.)

Из (24.1.) при х=0 получаем, что

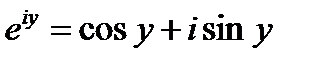
Отсюда следует, что любое комплексное число 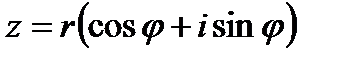, не равное нулю можем записать в виде

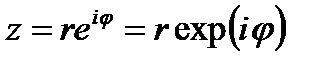(24.2.)