а) функция f(z)=ez=excosy+ieхsiny дифференцируема во всей комплексной плоскости. Так как
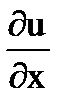 =excosy=
=excosy= 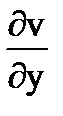 ,
, 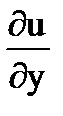 =-exsiny=-
=-exsiny=- 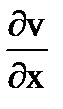
По формуле находим.
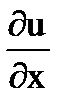 +i
+i 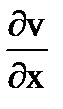 =excosy+iexsiny=ez,
=excosy+iexsiny=ez,
т.е.
(ez)=ez (25.14)
б) Функции sinz, cosz, shz, chz дифференцируемы во всей комплексной плоскости, и их производные вычисляются по формулам:
(sinz)¢=cosz, (cosz)¢=-sinz, (25.15)
(shz)¢=chz, (chz)¢=shz (25.16)
в) Рассмотрим функцию 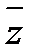 2=x2-y2-i2xy,
2=x2-y2-i2xy,
имеем 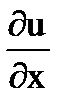 =2X,
=2X, 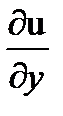 =-2y,
=-2y, 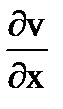 =-2y,
=-2y, 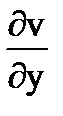 =+2x
=+2x
Условия (25.8) выполняются только при x=y=0, следовательно, функция 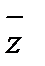 2 дифференцируема только в точке z=0
2 дифференцируема только в точке z=0
Пусть Z=rei  , тогда f(z)= U (z,
, тогда f(z)= U (z,  )+iV(z,
)+iV(z,  ), и условия Коши-Римана в полярных координатах имеют вид
), и условия Коши-Римана в полярных координатах имеют вид

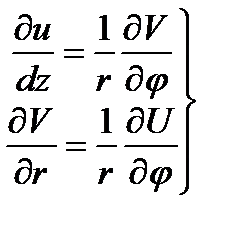 (25.17)
(25.17)
Следовательно,
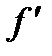 (z)=
(z)= 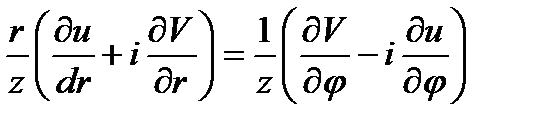 (25.18)
(25.18)
 2015-03-07
2015-03-07 634
634








