Интерполяционный полином Лагранжа. Пусть дана таблица значений. Требуется составить полином y=f(x) степени m 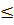 n-1, который принимал бы заданные значения yi при соответствующих значениях xi, т.е. yi=f(xi) (i=1,2,…n). Иными словами, график этого полинома должен проходить через заданные n точек Mi(xi,yi).
n-1, который принимал бы заданные значения yi при соответствующих значениях xi, т.е. yi=f(xi) (i=1,2,…n). Иными словами, график этого полинома должен проходить через заданные n точек Mi(xi,yi). 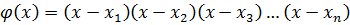 - вспомогательный многочлен n-ой степени, где xi – из таблицы. Формула для вычисления:
- вспомогательный многочлен n-ой степени, где xi – из таблицы. Формула для вычисления:
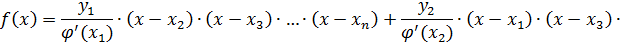
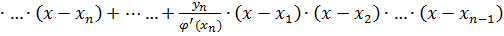 (37)
(37)
Интерполяционная формула Ньютона. Формулы конечных разностей:
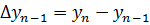 (38)
(38)
- разность первого порядка,
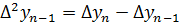 (39)
(39)
- разность второго порядка,
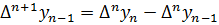 (40)
(40)
- разность 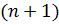 -го порядка.
-го порядка.
Имеем таблицу 1 конечных разностей.
Таблица 1 – Таблица конечных разностей
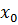 | 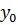 | ||||||
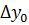 | |||||||
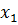 | 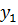 | 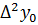 | |||||
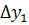 | 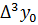 | ||||||
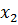 | 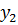 | 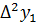 | 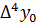 | ||||
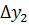 | 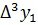 | 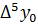 | |||||
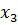 | 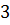 | 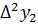 | 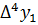 | … | |||
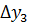 | 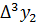 | … | |||||
| … | … | 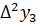 | … | ||||
| … | … | ||||||
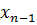 | 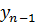 | … | |||||
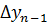 | |||||||
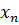 | 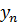 |
Формула Ньютона:
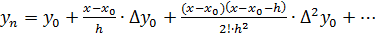 (41)
(41)
Рассмотрим типовые задания с подробными решениями.
Пример 1. Составить полином Лагранжа, удовлетворяющий таблице 2.
Таблица 2 – Данные задачи
| x | ||||
| y |
Вспомогательный многочлен: 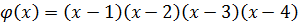 . Найдем его производную:
. Найдем его производную:
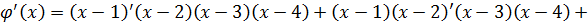
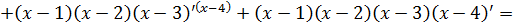
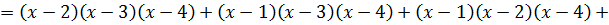
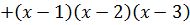 . Найдем значения производной при x из таблицы:
. Найдем значения производной при x из таблицы:
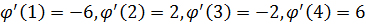 .
.
Подставляем полученные данные в формулу Ньютона: 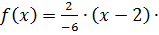
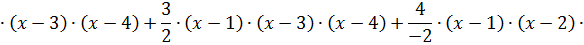
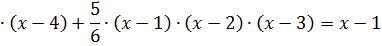
Пример 2. Данные представлены в таблице 3.
Таблица 3 – Данные задачи
| x | |||||||
| y |
Найти значение y при x=3,1, пользуясь интерполяционной формулой Ньютона.
Составим таблицу 4 конечных разностей.
Тогда, 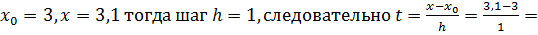
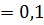 .
.
Напишем интерполяционный многочлен Ньютона 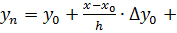
+ 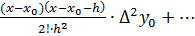
Получим 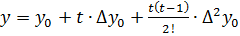 ;
;
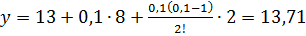 .
.
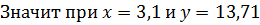 интерполяционный многочлен для этой таблицы:
интерполяционный многочлен для этой таблицы: 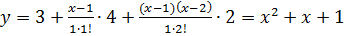 .
.
Таблица 4 – Таблица конечных разностей
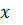 | 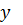 | 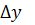 | 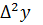 | 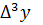 |
 2015-04-06
2015-04-06 1427
1427
