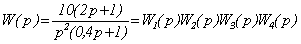Пример 3.1

.

Это передаточная функция последовательного соединения безынерционного усилительного звена W1(p)=10, двух интегрирующих звеньев W2(p)= 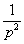, апериодического звена W3(p)= 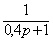и форсирующего звена с передаточной функцией W4(p)=2p+1.

Аналитическое выражение для ЛАЧХ этого соединения

L(w) = 20lg10 - 40lgw - 20lg 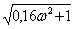+ 20lg .

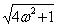Следует учесть, что строятся асимптотические ЛАЧХ. Построим их на рис. 3.15 и графически просуммируем. При построении учтем сопрягающие частоты wсопр1=1/2=0,5 с-1, wсопр2=1/0,4=0,25 с-1 и то, что ЛАЧХ двух интегрирующих звеньев (W2(p)= 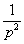) есть прямая с наклоном -40 дБ/дек, пересекающая ось нуля децибел (ось частот) при w=1 с-1. Результатом суммирования окажется ломаная линия, показанная на рис. 3.15.

Низкочастотная асимптота пройдет с наклоном -40 дБ/дек до сопрягающей частоты wсопр1=0,5 с-1 так, что ее продолжение будет зафиксировано в точке (w=1 с-1, L1(w)=20lg10=20 дБ). На первой сопрягающей частоте наклон асимптоты изменится на +20 дБ по сравнению с наклоном предыдущей асимптоты и составит - 20 дБ. На второй сопрягающей частоте wсопр2=0,25 с-1 наклон асимптоты изменится на - 20 дБ/дек по сравнению с наклоном предыдущей асимптоты и составит -4 0 дБ/дек.

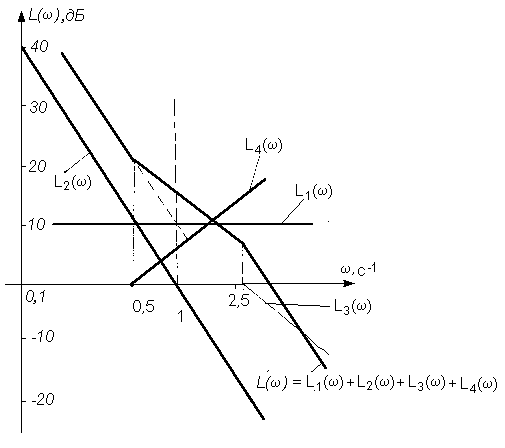
Рис. 3.15

Рассмотренное в примере 3.1 обоснование построения асимптотических ЛАЧХ последовательного соединения типовых динамических звеньев можно свести к следующим этапам:

1) По передаточной функции соединения звеньев находят 20lgK дБ и сопрягающие частоты wсопрi=1/Тi.

2) Проводят низкочастотную асимптоту:

а) горизонтально, если отсутствуют интегрирующие и идеальные дифференцирующие звенья (ордината этой горизонтали равна 20lgK дБ);

б) с наклоном - 20×n дБ/дек через точку с координатами (w=1 с-1, L(1)=20lgK дБ), если имеется n интегрирующих звеньев;

в) с наклоном + 20×m дБ/дек через точку с координатами (w=1 с-1, L(1)=20lgK дБ), если имеется m идеальных дифференцирующих звеньев.

3) На каждой сопрягающей частоте наклон асимптоты изменяется по отношению к наклону предыдущей асимптоты на:

- 20 дБ/дек - для апериодического звена,

-4 0 дБ/дек - для колебательного звена,

+20 дБ/дек - для форсирующего звена первого порядка W(p)= ,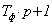

+40 дБ/дек - для форсирующего звена второго порядка
Wi(p) = .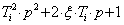

4) При необходимости производится уточнение асимптотической ЛАЧХ, что существенно при наличии колебательных звеньев с относительными коэффициентами x<0,5.

ЛФЧХ последовательного соединения строится на основании алгебраического суммирования ЛФЧХ звеньев, входящих в это соединение. В этом случае упростить построение не удается.

При использовании ЭВМ производится точное построение ЛАЧХ и ЛФЧХ. При этом необходимо задаться начальным и конечным значениями частоты и шагом ее изменения, при котором обеспечивается необходимое число расчетных точек в пределах каждой декады.

В заключение отметим, что частотные характеристики позволяют судить о влиянии на динамические свойства систем тех или иных звеньев и осуществлять анализ и синтез систем автоматического управления. Поэтому ЛАЧХ и ЛФЧХ необходимо строить на одном графике.