Введение в теорию устойчивости линейных стационарных САУ

Рассмотрим математическую сущность устойчивости и неустойчивости линейных стационарных САУ. Согласно данному выше физическому определению устойчивость зависит только от характера свободного движения системы. Свободное движение линейной или линеаризованной системы описывается однородным дифференциальным уравнением

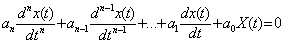, (4.1)

где x(t) = xсв(t) - свободная составляющая выходной величины системы.

Вынужденная составляющая выходной величины, зависящая от вида внешнего воздействия и правой части дифференциального уравнения (2.1), на устойчивость системы не влияет.

Математическое определение понятия “устойчивость”

Система является устойчивой, если свободная составляющая xсв(t) переходного процесса с течением времени стремится к нулю, т.е. если

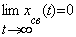(4.2)

Очевидно, что при этом выходная величина системы будет стремиться к вынужденной составляющей, определяемой правой частью уравнения (2.1). Устойчивость в смысле условия (4.2) принято называть асимптотической.

Если свободная составляющая неограниченно взрастает, т.е. если

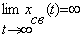, (4.3)

то система неустойчива.

Наконец, если свободная составляющая не стремится ни к нулю, ни к бесконечности, то система находится на границе устойчивости.

Найдем общее условие, при котором система, описываемая уравнением (4.1), устойчива. Решение уравнения (4.1)

xсв(t) = 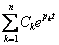, (4.4)

где Ck - постоянные интегрирования, зависящие от начальных условий;

pk - корни характеристического уравнения

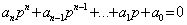. (4.5)

Корни характеристического уравнения могут быть действительными (pk=ak), мнимыми (pk=jbk) и комплексными

pk=ak ± jbk, (4.6)

причем как комплексные, так и мнимые корни попарно сопряжены.

Свободная составляющая (4.4) удовлетворяет условию устойчивости, если каждое слагаемое вида 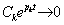. Характер этой функции времени зависит от вида корня pk.

Рассмотрим все возможные случаи расположения корней характеристическо­го уравнения на комплексной плоскости (рис. 4.1) и соответствующие им функции xсв(t), которые показаны внутри кругов (как на экране осциллографа)

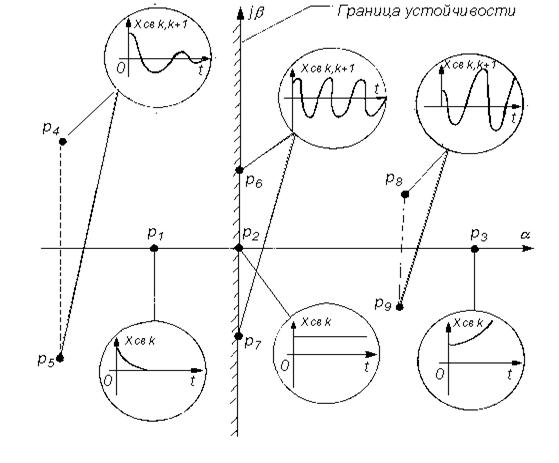
Рис. 4.1. Влияние корней характеристического уравнения на составляющие ее