Свободного движения

1) Каждому действительному корню pk=ak в решении (4.4) соответствует слагаемое вида

xсвk(t) = 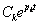. (4.7)

Если ak<0 (корень p1), то функция (4.7) плавно стремится к нулю. Если ak>0 (корень p3), то функция (4.7) неограниченно возрастает. Если ak=0 (корень p2), то эта функция остается постоянной.

2) Каждой паре сопряженных комплексных корней pk=ak+jbk и pk+1=ak‑jbk в решении (4.4) соответствуют два слагаемых, которые могут быть объединены в одно слагаемое

xсвk(t) = 2 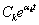sin(bkt+yk). (4.8)

Функция (4.8) представляет собой синусоиду с частотой bk и амплитудой, изменяющейся по экспоненте. Если ak < 0 (корни p4 и p5 на рис. 4.1), то колебательная составляющая (рис. 4.1) будет затухать.

Если ak > 0 (корни p8 и p9),то амплитуда колебаний будет неограниченно возрастать. Наконец, если ak = 0 (корни p6 и p7), т.е. оба сопряженных корня - мнимые (pk=jbk, pk+1=-jbk), то xсвk(t)=2 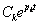sin(bkt+yk) - незатухающая синусоида bk.

Если среди корней характеристического уравнения (4.5) имеются l равных между собой корней pl, то в решении (4.4) вместо l слагаемых вида 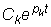появится одна составляющая

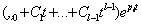. (4.9)

Учитывая, что функция вида 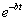при любом b убывает быстрее, чем возрастают слагаемые вида 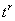, можно доказать, что и в случае кратности корней решение (4.4) будет стремиться к нулю лишь при отрицательности действительной части кратных корней pl.

На основании проведенного анализа можно сформулировать общее условие устойчивости:

для устойчивости линейной стационарной САУ необходимо и достаточно, чтобы действительные части всех корней характеристического уравнения системы были отрицательными.

При этом действительные корни рассматриваются как частный случай комплексных корней, у которых мнимая часть равна нулю. Если хотя бы один корень имеет положительную действительную часть, то система будет неустойчивой.

Устойчивость системы зависит только от вида корней характеристического уравнения и не зависит от характера внешних воздействий на систему. Устойчивость есть внутреннее свойство системы, присущее ей вне зависимости от внешних условий.

Используя геометрическое представление корней (4.6) на комплексной плоскости (см. рис. 4.1) в виде векторов или точек, можно дать вторую формулировку общего условия устойчивости (эквивалентную основной):

для устойчивости линейной стационарной САУ необходимо и достаточно, чтобы все корни характеристического уравнения находились в левой полуплоскости.

Если хотя бы один корень находится в правой полуплоскости, то система будет неустойчивой.

Мнимая ось jb (рис. 4.1) является границей устойчивости в плоскости корней. Если характеристическое уравнение имеет одну пару мнимых корней (pk=jbk, pk+1=-jbk), то в системе устанавливаются незатухающие гармонические колебания с круговой частотой w = çbkç. В этом случае система находится на колебательной границе устойчивости.

Точка b = 0 на мнимой оси соответствует так называемому нулевому корню. Если характеристическое уравнение имеет один нулевой корень, то система находится на апериодической границе устойчивости. Если таких корня два, то система неустойчива (два последовательно соединенных интегрирующих звена создают сдвиг по фазе -180° при всех значениях частот).

Таким образом, для суждения об устойчивости линейной стационарной САУ достаточно определить знаки действительных частей корней характеристического уравнения. Но для этого необходимо вычислять корни характеристического уравнения.

В ТАУ разработан ряд методов, с помощью которых можно судить о том, имеются ли корни с положительной действительной частью, не находя числовые значения самих корней. Эти методы называются критериями устойчивости.

Простейшим критерием устойчивости является условие положительности коэффициентов характеристического уравнения. Положительность коэффициентов уравнения (4.4) является необходимым (но не достаточным!) условием устойчивости системы. Это означает, что если все коэффициенты характеристического уравнения положительны, то система может быть устойчивой и неустойчивой (при порядке системы n>2). Но если хотя бы один коэффициент уравнения отрицателен или равен нулю, то система неустойчива.

Критерии устойчивости могут быть алгебраическими и частотными. Алгебраические критерии устанавливают необходимые и достаточные условия отрицательности корней в форме ограничений, накладываемых на определенные комбинации коэффициентов характеристического уравнения.

Частотные критерии определяют связь между устойчивостью системы и формой ее частотных характеристик.