2015-03-07
266
Систему уравнений (17), (20), (21) интегрируем численным методом на интервале времени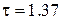 
с. Используя конечно-разностную схему Эйлера. Шаг интегрирования 
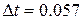с.
Начальные условия по переменным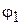 
, 
, 
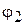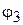.приведены в исходных данных, а по переменным 
, 
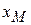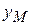вычисляются оп формулам (рис. 1)
 ;
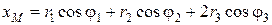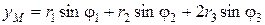
| (22) |
Подставив в (22) числовые значения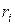 
, 
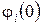, получи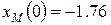м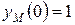 
м, 
м.
Программа представлена на листинге 1.
Обозначения переменных в программе:
| Переменные |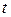 
| 
| 
| 
| 
| 
| 
| 
| 
|
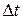
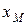
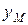
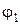
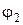
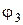
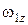
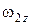
| Обозначение | t | dt | Xm | Ym | fi1 | fi2 | fi3 | fi4 | fi5 |
| Переменные |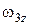 
| 
| 
| 
| 
| 
| 
| 
| 
|
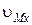
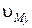
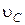
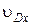
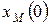
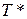
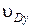
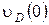
| Обозначение | w1 | w2 | w3 | Vcx | Vdx | Xm0 | Tc | Vdy | Vd0 |
По результатам моделирования на рис. 3 -5 построены графики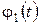 
,, 
, 
, 
, 
, 
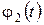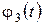
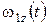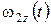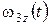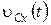и траектории сближения точек M и D.
