Листинг 1

function kinematik

R1 = 0.953; R2 = 0.847; R3 = 0.457; Vd = 0.304; dt = 0.057; Tc = 0.297;

delta = 0.01; fi10 = 1.63; fi20 = 3.37; fi30 = 2.87;

Xd0 = -2.15; Yd0 = 1.18; alf = 4.35;

Xd = Xd0; Yd = Yd0; fi1 = fi10; fi2 = fi20; fi3 = fi30;

[Xm0,Ym0] = get_Xm_Ym(R1,R2,R3,fi10,fi20,fi30);

Xm = Xm0; Ym = Ym0; Vdx = Vd*cos(alf); Vdy = Vd*sin(alf); dR = 1; i=1; t=0;

while (dR > delta),

[Vmx,Vmy] = get_Vmx_Vmy(Xm,Ym,Xd0,Yd0,Vdx,Vdy,Tc,t);

[w1,w2,w3,Vcx] = get_w1_w2_w3_Vcx(R1,R2,R3,fi1,fi2,fi3,Vmx,Vmy);

XmV(i) = Xm; YmV(i) = Ym; XdV(i) = Xd; YdV(i) = Yd;

VcxV(i) = Vcx; VmxV(i) = Vmx; VmyV(i) = Vmy;

tV(i) = t; w1V(i) = w1; w2V(i) = w2; w3V(i) = w3;

fi1V(i) = fi1; fi2V(i) = fi2; fi3V(i) = fi3;

Xm = Xm + Vmx*dt; Ym = Ym + Vmy*dt; Xd = Xd + Vdx*dt; Yd = Yd + Vdy*dt;

fi1 = fi1 + w1*dt; fi2 = fi2 + w2*dt; fi3 = fi3 + w3*dt;

t = t + dt; i=i+1; dR = sqrt((Xm - Xd)^2+(Ym - Yd)^2);

end;

plot(tV,VcxV,'k'); plot(tV,w1V,'k--',tV,fi1V,'k');

plot(tV,w2V,'k--',tV,fi2V,'k'); plot(tV,w3V,'k--',tV,fi3V,'k');

plot(XmV,YmV,'k:',XdV,YdV,'k-.',Xd0,Yd0,'kv',XmV(1),YmV(1),'ko',
XmV(length(YmV)),YmV(length(YmV)),'ko',XdV(length(XdV)),YdV(length(XdV)),'kv');

function [Xm, Ym] = get_Xm_Ym(R1,R2,R3,fi1,fi2,fi3)

Xm = R1*cos(fi1) + R2*cos(fi2) + 2*R3*cos(fi3);

Ym = R1*sin(fi1) + R2*sin(fi2) + 2*R3*sin(fi3);

function [Vmx,Vmy] = get_Vmx_Vmy(Xm,Ym,Xd0,Yd0,Vdx,Vdy,Tc,t)

Vmx = Vdx + (Xd0 + Vdx*t - Xm)/Tc;

Vmy = Vdy + (Yd0 + Vdy*t - Ym)/Tc;

function [w1,w2,w3,Vcx] = get_w1_w2_w3_Vcx(r1,r2,r3,fi1,fi2,fi3,Vmx,Vmy)

w3 = Vmy/(r3*(2*cos(fi3) + sin(fi3)));

Vcx = Vmx + w3*r3*(2*sin(fi3) - cos(fi3));

w1 = (Vcx*cos(fi2) + w3*r3*cos(fi3-fi2))/(r1*sin(fi2-fi1));

w2 = (w3*r3*sin(fi3) - w1*r1*cos(fi1))/(r2*cos(fi2));

ЛИТЕРАТУРА

Основная

1. Промышленная робототехника / Л.С.Ямпольский, В.А. Якимович, Е.Г. Вайсман и др.; Под. ред. Л.С.Ямпольского. – Киев: Техника, 1984.

2. Робототехника и гибкие автоматизированные производства/ Под. ред. И.М. Макарова. Кн.3. Управление робототехническими системами и ГАП. – М.: ВШ, 1986.

3. Медведев В.С., Лесков А.Г., Ющенко А.С. Системы управления манипуляционными роботами. – М.: Наука, 1978.

Дополнительная

4. Яблонский А.А., Никифорова В.М. Курс теоретической механики. – Ч.I,: М.: Наука, 1984.

5. Васильева А.В., Бутузов В.Ф. Асимптотическое разложение решений сингулярно-возмущенных уравнений.- М.: Наука, 1973.

Приложение 1

Вариант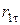
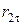
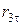
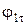
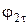
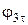
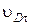
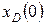
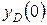
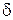
	0.82	0.68	0.46	2.9	1.1	0.5	0.508	-0.15	1.85	0.011
	0.81	0.47	0.91	1.3	2.2	3.6	0.308	-0.94	1.71	0.012
	0.43	0.91	0.84	0.3	3.8	4.2	0.512	-0.42	0.25	0.013
	0.42	0.97	0.88	2.8	0.2	5.7	0.462	-0.21	1.22	0.014
	0.78	0.45	0.81	1.7	0.1	5.8	0.385	1.35	1.51	0.015
	0.71	0.89	0.76	4.6	0.1	1.6	0.312	1.33	-1.20	0.016
	0.46	0.97	0.74	1.3	4.3	5.6	0.421	-0.61	-0.24	0.017
	0.81	0.72	0.48	1.1	3.0	3.3	0.472	-1.38	1.61	0.018
	0.76	0.79	0.45	0.3	2.4	1.8	0.465	0.54	1.02	0.019
	0.72	0.49	0.78	0.5	4.2	3.6	0.375	1.61	-0.55	0.020
	0.83	0.57	0.49	0.5	1.6	3.0	0.525	-0.92	1.78	0.021
	0.68	0.46	0.83	3.9	4.9	0.3	0.310	0.46	-2.04	0.022
	0.78	0.85	0.49	2.1	1.0	0.1	0.460	0.51	1.65	0.023
	0.48	0.97	0.73	0.3	1.8	3.7	0.402	0.26	1.30	0.024
	0.42	0.97	0.78	0.3	2.9	0.4	0.455	0.45	1.12	0.025
	0.51	0.82	0.79	3.2	4.1	3.0	0.288	-1.57	0.13	0.026
	0.41	0.83	0.98	2.0	4.3	1.4	0.451	-1.18	0.56	0.027
	0.82	0.45	0.78	1.6	2.9	0.4	0.312	-0.99	0.52	0.028
	0.92	0.98	0.81	1.5	2.7	1.7	0.294	-1.43	1.95	0.029
	0.79	0.68	0.48	4.1	5.8	1.1	0.306	0.41	-1.43	0.030
	0.76	0.42	0.85	5.2	0.4	2.3	0.380	0.84	0.26	0.031
	0.75	0.78	0.47	1.1	2.8	2.0	0.515	-1.66	0.42	0.032
	0.71	0.49	0.82	4.9	0.1	1.9	0.385	0.62	0.12	0.033
	0.75	0.6	0.78	0.3	1.9	0.1	0.398	1.11	1.32	0.034
	0.68	0.79	0.82	2.3	0.7	0.5	0.392	1.40	1.67	0.035
	0.81	0.72	0.49	3.7	5.4	4.2	0.371	0.13	-1.98	0.036
	0.78	0.65	0.48	1.6	0.1	1.5	0.275	0.31	1.62	0.037
	0.45	0.97	0.78	0.9	0.5	3.9	0.290	1.22	0.78	0.038
	0.49	0.98	0.77	2.1	0.4	3.7	0.305	0.21	0.72	0.039
	0.72	0.75	0.49	3.9	5.4	0.3	0.340	1.14	-1.25	0.040

Приложение 2

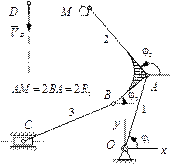
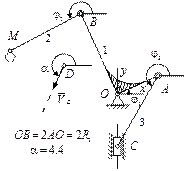
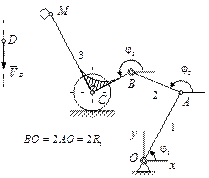
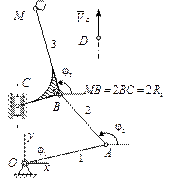
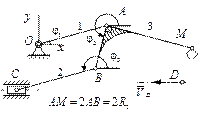
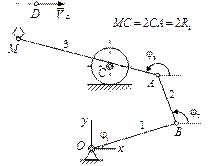
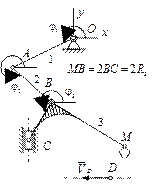
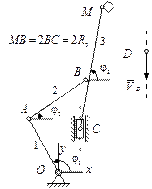
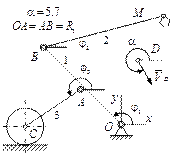
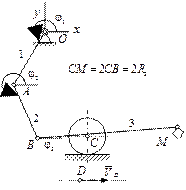
Приложение 3