При рассмотрении СМО будем использовать следующие обозначения:
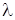 – интенсивность входящего потока требований;
– интенсивность входящего потока требований;
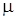 – интенсивность обслуживания требований одним прибором;
– интенсивность обслуживания требований одним прибором;
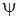 – коэффициент использования обслуживающих приборов системы;
– коэффициент использования обслуживающих приборов системы;
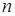 – число требований в СМО. Это число будем называть состоянием системы;
– число требований в СМО. Это число будем называть состоянием системы;
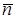 – математическое ожидание (м.о.) числа требований в СМО;
– математическое ожидание (м.о.) числа требований в СМО;
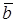 – м.о. числа требований в очереди СМО;
– м.о. числа требований в очереди СМО;
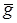 – м.о. числа свободных приборов в СМО;
– м.о. числа свободных приборов в СМО;
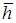 – м.о. числа занятых приборов в СМО;
– м.о. числа занятых приборов в СМО;
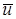 – м.о. длительности пребывания требований в СМО;
– м.о. длительности пребывания требований в СМО;
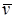 – м.о. длительности обслуживания требований прибором
– м.о. длительности обслуживания требований прибором 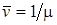 ;
;
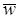 – м.о. длительности пребывания требований в очереди СМО;
– м.о. длительности пребывания требований в очереди СМО;
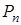 – стационарная вероятность пребывания в СМО точно
– стационарная вероятность пребывания в СМО точно 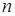 требований.
требований.
Приведем несколько наиболее важных соотношений
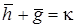 ,
, 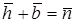 ,
, 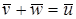 .
.
К этим соотношениям можно добавить закон сохранения среднего потока требований, согласно которому в стационарном режиме СМО интенсивность входного потока равна интенсивности выходящего потока.
Большое значение для исследования открытых систем, когда входящие требования независимы от входящих, имеет формула Литтла
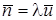 ,
, 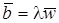 .
.
Система 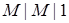
Система 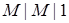 содержит один прибор, длительность обслуживания имеет экспоненциальное распределение с параметром
содержит один прибор, длительность обслуживания имеет экспоненциальное распределение с параметром 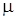 ; в систему поступает пуассоновский поток требований, длительность интервала между последовательными требованиями имеет экспоненциальное распределение с параметром
; в систему поступает пуассоновский поток требований, длительность интервала между последовательными требованиями имеет экспоненциальное распределение с параметром 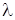 ; входящие в систему требования поступают в очередь неограниченной длины; очередное требование на обслуживание выбирается из очереди по правилу
; входящие в систему требования поступают в очередь неограниченной длины; очередное требование на обслуживание выбирается из очереди по правилу 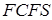 .
.
Система 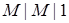 – простейшая нетривиальная система, представляющая интерес. Она может быть описана с помощью процесса гибели и размножения, если предположить интенсивности
– простейшая нетривиальная система, представляющая интерес. Она может быть описана с помощью процесса гибели и размножения, если предположить интенсивности 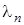 и
и 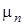 постоянными, то есть
постоянными, то есть 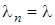 ,
, 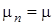 для всех значений
для всех значений 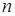 . Пространство состояний является счетным.
. Пространство состояний является счетным.
Подставляя значения интенсивностей 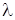 и
и 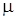 в равенство
в равенство
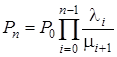 ,
, 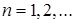 , (1)
, (1)
получим
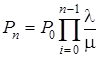 , или
, или 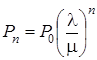 ,
, 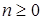 . (2)
. (2)
Необходимое и достаточное условие существования стационарного режима системы 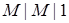 просто сводится к выполнению неравенства
просто сводится к выполнению неравенства  . Из выражения
. Из выражения
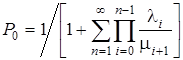
определим
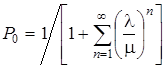 .
.
Так как  , используя равенство
, используя равенство
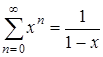 ,
,
имеем
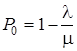 .
.
Обозначив через 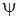 коэффициент использования системы, получим, что для системы
коэффициент использования системы, получим, что для системы 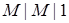 коэффициент
коэффициент 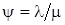 . Следовательно, согласно условию стационарности требуется, чтобы
. Следовательно, согласно условию стационарности требуется, чтобы 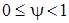 . Из равенства (2) окончательно определим, что
. Из равенства (2) окончательно определим, что
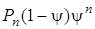 ,
, 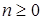 .
.
Важной характеристикой СМО является м.о. числа требований 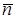 , пребывающих в системе. Принимая во внимание равенство
, пребывающих в системе. Принимая во внимание равенство
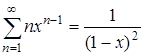 ,
,
запишем
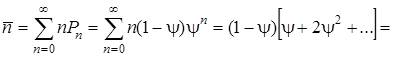
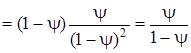 .
.
Таким образом,
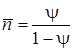 .
.
Число требований, находящихся в очереди, очевидно, 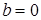 , если
, если 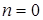 и
и 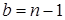 , если
, если 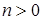 . Вероятность того, что в очереди находится
. Вероятность того, что в очереди находится 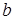 требований равна
требований равна 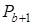 при
при 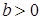 , а при
, а при 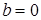 она равна
она равна 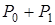 . Следовательно,
. Следовательно,
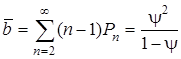 .
.
Из формулы Литтла 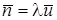 и
и 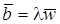 получим
получим
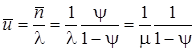 ,
,
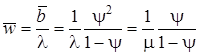 .
.
Система 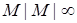
Рассмотрим систему, в которой всегда имеется свободный прибор для каждого вновь поступающего требования. В частности, положим 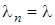 ,
, 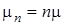 . Из равенства (1) имеем
. Из равенства (1) имеем
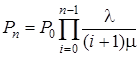 , или
, или 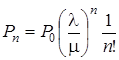 ,
, 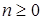 .
.
Вероятность
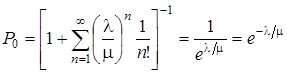 .
.
Таким образом,
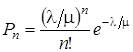 ,
, 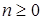 .
.
Следовательно, число требований, находящихся в системе, описывается распределением Пуассона.
Математическое ожидание числа требований в системе
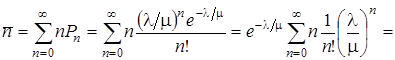
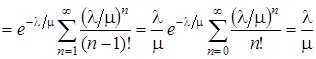 .
.
Заметим, что выражение 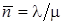 можно вывести из формулы Литтла
можно вывести из формулы Литтла 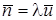 , учитывая, что
, учитывая, что 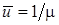 .
.
Условие существования стационарного режима СМО в данном случае задается неравенством 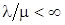 .
.
 2015-03-27
2015-03-27 560
560








