2015-03-07
2946
Многие стационарные, т.е. не изменяющиеся во времени физические процессы описываются уравнениями эллиптического типа, в простейшем случае (однородной среды и отсутствия источников) – уравнением Лапласа, которое для трех направлений координат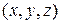 
можно записать в виде:
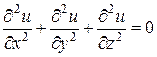, (4.1)
где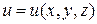 
– искомая функция координат.
В операторной форме уравнение Лапласа может быть представлено следующим образом:
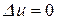, (4.2)
где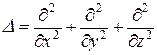 
– оператор Лапласа.
В общем случае (неоднородная среда и наличие источников внутри рассматриваемой области) аналогичные физические процессы описываются уравнением Пуассона, которое в векторной форме имеет вид:
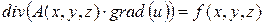, (4.3)
где 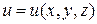– искомая функция; 
, 
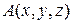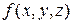– некоторые функции независимых переменных.
Уравнение (4.3) может быть записано в частных производных как:
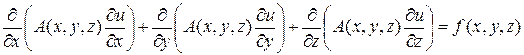, (4.4)
или в операторной форме как:
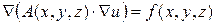, (4.5)
где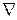 
– оператор Наббла, определяемый выражением:
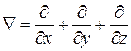. (4.6)
Из выражений (4.3) – (4.5) видно, что уравнение Пуассона является обобщением уравнения Лапласа для случая отличной от нуля правой части. Покажем это на примере задачи о распространении стационарного теплового поля.
Рассмотрим задачу о стационарном распределении тепла в некотором объеме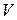 
, ограниченном замкнутой поверхностью 
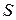трехмерного пространства 
.
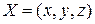Процесс теплопроводности или кондукции определяется законом Фурье, согласно которому вектор плотности теплового потока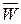 
пропорционален градиенту температуры 
:
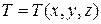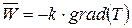, (4.7)
где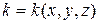 
– коэффициент теплопроводности.
Плотность теплового потока равна количеству теплоты, протекающему в единицу времени через единичную площадь изотермической поверхности.
Как правило, цель стационарной задачи теплопроводности сводится к необходимости нахождения зависимости температуры от координат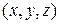 
при известном распределении плотности источников тепла 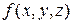. Поскольку функция 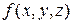не входит непосредственно в уравнение Фурье (4.7), необходимо выполнить ряд предварительных преобразований.
Из приведенного выше определения плотности теплового потока следует, что суммарное количество тепла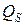 
, прошедшее в единицу времени через замкнутую поверхность 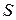, ограничивающую объем 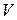, в общем случае выражается интегралом:
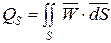, (4.8)
где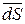 
– вектор, модуль которого численно равен площади 
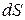соответствующего бесконечно малого элемента поверхности, а направление совпадает с направлением нормали к этому элементу; 
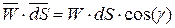– скалярное произведение векторов 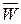и ;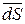 
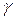– угол между ними.
Суммарное количество тепла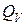 
, выделяющееся в единицу времени в объеме 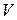, ограниченном поверхностью 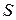, определяется интегралом:
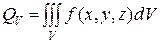. (4.9)
В данном случае уравнение баланса тепла должно отражать факт равенства количества тепла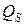 
и количества тепла :
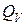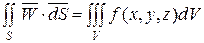. (4.10)
Согласно теореме Остроградского-Гаусса:
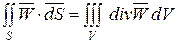. (4.11)
Тогда, подставив (4.11) в (4.10), получим:
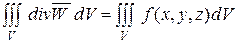; (4.12)
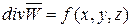. (4.13)
Подставляя в уравнение (4.13) закон Фурье (4.7), получим уравнение для стационарной задачи теплопроводности в векторной форме:
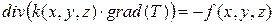. (4.14)
Если источники тепла отсутствуют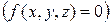 
и среда однородна 
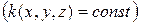, уравнение (4.14) можно переписать в виде:
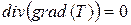. (4.15)
Учитывая, что по определению градиент некоторого скалярного поля 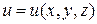определяется выражением:
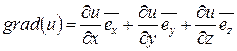, (4.16)
где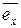 
, 
, 
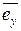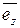– единичные векторы (орты) в направлениях соответствующих координатных осей, а дивергенция некоторого векторного поля 
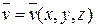– выражением:
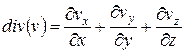, (4.17)
где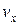 
, 
, 
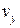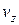– проекции вектора 
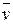на соответствующие оси координат, уравнение (4.15) можно переписать в частных производных:
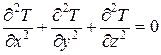(4.18)
или в операторной форме:
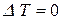, (4.19)
т.е. в виде уравнения Лапласа.
При наличии в объеме 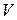источников тепла 
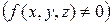и в случае неоднородной среды 
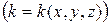уравнение (4.14) в частных производных можно переписать в виде:
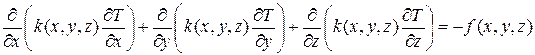, (4.20)
или в операторной форме:
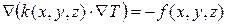. (4.21)
Если среда однородна 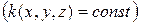, то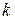 
можно вынести за знак частной производной в выражении (4.20) или за знак оператора Наббла в выражении (4.21). В результате получим частный случай уравнения Пуассона в виде:
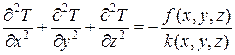, (4.22)
или в операторной форме:
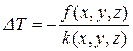. (4.23)
Таким образом, сравнивая уравнения (4.19) и (4.23), можно сделать вывод, что уравнение Лапласа является частным случаем уравнения Пуассона для случая равенства нулю правой части (отсутствие источников и однородность среды).
