2015-03-07
912
Пусть область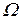 
ограничена поверхностью 
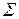(рис. 4.1).
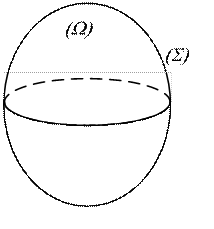
Рис. 4.1. Ограниченная область трехмерного пространства
Типичной для уравнения Лапласа является задача: найти функцию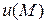 
, 
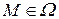, гармоническую в 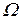и удовлетворяющую на 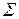граничному условию, которое может быть одного из следующих видов:
1. 
, 
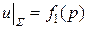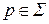, – первая краевая задача, или задача Дирихле;
2. 
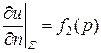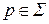, , – вторая краевая задача, или задача Неймана;
3. 
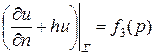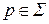, , – третья краевая задача.
Здесь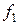 
, 
, 
, 
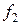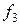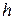– заданные функции; 
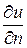– производная в направлении внешней нормали к поверхности .
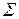Геометрический смысл задачи Дирихле для одномерного уравнения Лапласа тривиален. Одномерные гармонические функции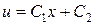 
суть прямые линии, и задача Дирихле сводится к следующей: провести прямую через две точк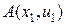и 
и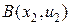 
(рис. 4.2).
В зависимости от того, где ищется решение задачи – внутри области, ограниченной поверхностью 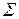или в области, расположенной вне поверхности 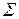, различают внутренние и внешние краевые задачи для уравнения 
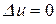. Если границей области является плоскость, то говорят, что граничная задача ставится для полупространства (пример: задача о тепловом состоянии однородного тела – внутренняя задача Дирихле, а электростатическая задача – внешняя).
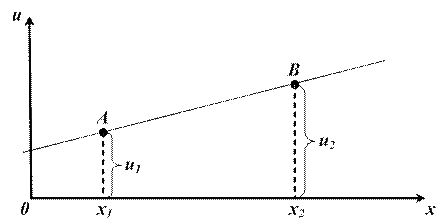
Рис. 4.2. Геометрический смысл задачи Дирихле для одномерного уравнения Лапласа
