2015-03-07
2121
Решить методом Фурье задачу:
, 
, 
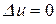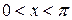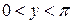(4.50)
при граничных условиях:
, 
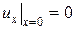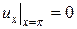(4.51)
, 
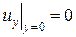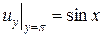. (4.52)
Согласно методу Фурье, ищем частные решения уравнения (1) в виде:
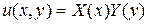. (4.53)
Подставляя (4.53) в (4.50), имеем:
, 
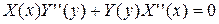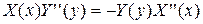
делим обе части на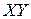 
, получаем:
,
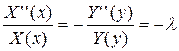откуда получаем два уравнения:
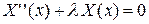, (4.54)
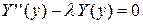. (4.55)
Чтобы получить нетривиальное решение уравнения (4.50) вида (4.53), удовлетворяющее граничным условиям (4.51), необходимо найти нетривиальное решение уравнения (4.54), удовлетворяющее граничным условиям:
, 
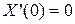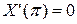. (4.56)
Таким образом, для определения функций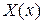 
приходим к задаче о собственных значениях: найти решения линейного дифференциального уравнения второго порядка с заданными граничными условиями:
, , 
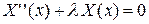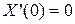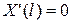. (4.57)
Будем искать частные решения в ви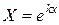де:
, где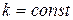 
,
тогда
, 
.
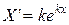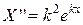Подставляя полученные выражения производных в уравнение (4.54), находим:
, 
.
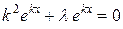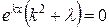Так как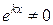 
, то, значит:
.
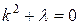Следовательно, если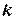 
будет удовлетворять данному уравнению, 
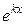будет решением уравнения (4.54). Полученное уравнение называется характеристическим по отношению к уравнению (4.54). Корни характеристического уравнения комплексные (чисто мнимые). Обозначим их:
, 
,
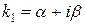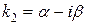где
, 
.
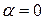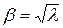Решения можно записать в форме:
, 
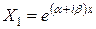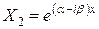или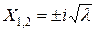 
.
Перепишем эти комплексные решения в виде суммы действительной и мнимой части:
, 
.
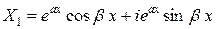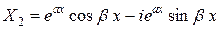Общее решение уравнения (4.54) будет:
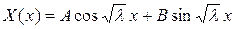, (4.58)
где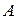 
, 
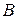– произвольные постоянные.
Подберем теперь постоянные 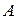и 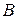так, чтобы удовлетворялось условие (4.51). Так как 
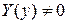(иначе будет 
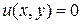, что противоречит поставленному условию), то функция 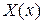должна удовлетворять условиям (4.51). Найдем производную функции :
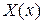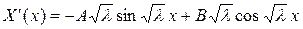. (4.59)
Подставляя значения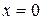 
и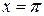 
в равенство (4.59) получаем:
.
.
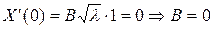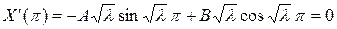Из последнего уравнения следует: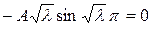 
. 
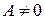, так как иначе 
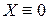и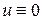 
, что противоречит условию, 
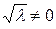, так как уравнение теряет смысл. Следовательно, должно быть 
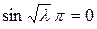, откуда 
, 
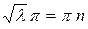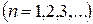, получили:
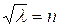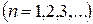, . (4.60)
Этим собственным числам соответствуют собственные функции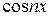 
. Таким образом, получаем:
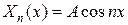. (4.61)
Найдем общее решение уравнения (4.55).
Составим характеристическое уравнени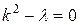е: 
, где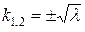 
.
Корни характеристического уравнения действительные и различны. В этом случае частными решениями будут функции:
, 
.
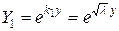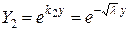Следовательно, общий интеграл имеет вид:
.
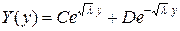Значениям параметра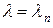 
соответствуют решения уравнения (4.55):
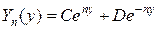, (4.62)
где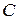 
, 
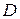– произвольные постоянные.
Подставим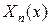 
и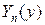 
в (4.53), получим:
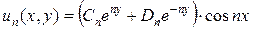. (4.63)
Уравнение (4.63) удовлетворяет уравнению (4.50) и граничным условиям (4.51) при любых постоянных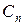 
, 
.
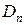Сумма решений – решение уравнения (4.50), поэтому:
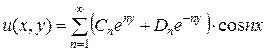. (4.64)
Решение (4.64) должно удовлетворять граничным условиям (4.52):
;
;
.
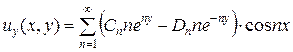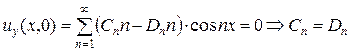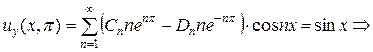
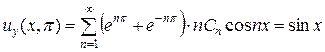Написанный ряд представляет собой разложение заданной функции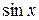 
в ряд Фурье по косинусам в промежутке 
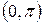. Коэффициенты 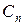определяются по известной формуле:
;
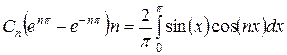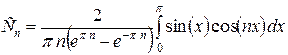. (4.65)
