Решение I

Будем искать нетривиальные решения вида 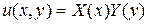задачи 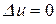, , 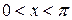, 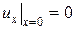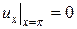. При этом придем к задаче Штурма-Лиувилля (см. Приложение №1): , , .

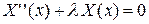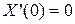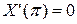Собственные значения и собственные функции, которой будут:

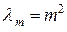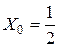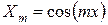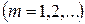, , , . (4.69)

Аналогично, если мы будем искать нетривиальные решения вида 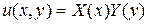задачи 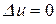, , 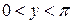, , 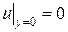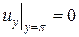то мы придем к задаче Штурма-Лиувилля (см. Приложение №1): , , .

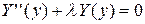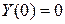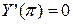Собственные значения и собственные функции этой задачи будут:

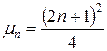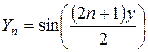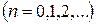, , . (4.70)

Так как в случае а) 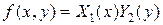, то мы будем искать решение в виде 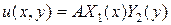. Тогда условия (4.67), (4.68) будут выполнены автоматически. Подставляя 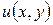в (4.66), найдем .

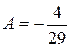Итак, в случае а) получаем:

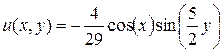. (4.71)

В случае b) 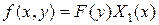, где 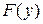не является собственной функцией нужной задачи Штурма-Лиувилля, поэтому решение следует искать в виде:

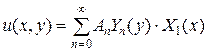, (4.72)

для чего заданную функцию 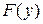следует также разложить в ряд Фурье по собственным числам 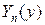и найти коэффициент разложения :

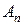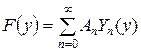. (4.73)

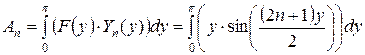. (4.74)

В случае с) мы будем искать решение в виде двойного ряда Фурье:

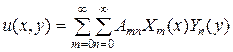. (4.75)

Для этого разложим правую часть – функцию 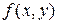– также в двойной ряд Фурье:

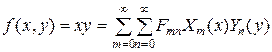. (4.76)

С учетом разложения в ряд Фурье, получим:

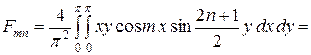
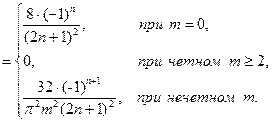
Подставляя (4.75), (4.76) в (4.66), найдем:

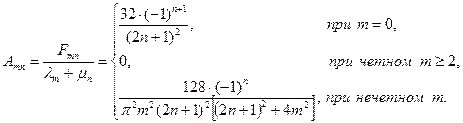
Поэтому в случае с) решением задачи будет:

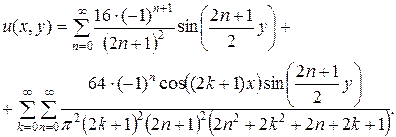(4.77)