Поскольку в случае b) 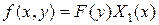 , где
, где 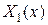 – собственная функция нужной задачи Штурма-Лиувилля, то мы будем искать решение в виде
– собственная функция нужной задачи Штурма-Лиувилля, то мы будем искать решение в виде 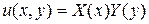 с неизвестной функцией
с неизвестной функцией 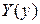 . Условие (4.67) будет выполнено автоматически, а (4.66) и (4.68) дадут дифференциальное уравнение для
. Условие (4.67) будет выполнено автоматически, а (4.66) и (4.68) дадут дифференциальное уравнение для 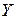 :
:
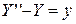 (4.78)
(4.78)
и граничные условия для него:
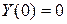 ,
, 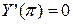 . (4.79)
. (4.79)
Общее решение уравнения (4.78) имеет вид:
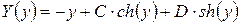 , (4.80)
, (4.80)
находя из граничных условий (4.79) 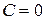 ,
, 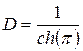 , получим окончательно, что
, получим окончательно, что
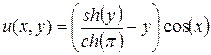 (4.81)
(4.81)
будет решением задачи в случае b).
В случае с) решение следует искать в виде:
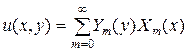 , (4.82)
, (4.82)
где 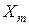 – собственные функции нужной задачи Штурма-Лиувилля, а
– собственные функции нужной задачи Штурма-Лиувилля, а 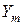 – неизвестные функции.
– неизвестные функции.
Для этого представим правую часть в аналогичном виде:
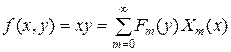 . (4.83)
. (4.83)
С учетом разложения в ряд Фурье получим:
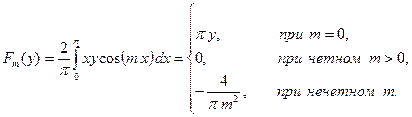
Подставляя уравнения (4.82), (4.83) в задачу (4.66), (4.68) мы получим обыкновенное дифференциальное уравнение:
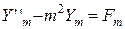 (4.84)
(4.84)
и граничные условия для него:
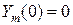 ,
, 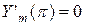 . (4.85)
. (4.85)
Условие (4.67) автоматически выполняется.
Решая граничную задачу (4.84), (4.85), находим, что:
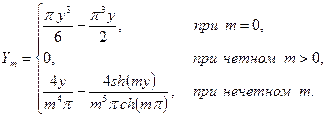
Поэтому решение задачи в случае с) есть:
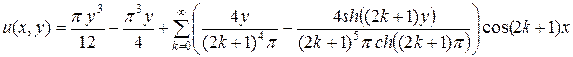 .(4.86)
.(4.86)
Можно было бы искать решение в виде (4.82), но с 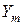 – собственными функциями нужной задачи Штурма-Лиувилля и неизвестными функциями
– собственными функциями нужной задачи Штурма-Лиувилля и неизвестными функциями 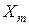 .
.
|
|
|
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Тихонов А.Н., Самарский А.А. Уравнения математической физики: Учебник. 7-е изд. – М.: Изд-во МГУ, 2004. – 798 с.
2. Свешников А.Г., Боголюбов А.Н., Кравцов В.В. Лекции по математической физике: Учебное пособие. 2-е изд., испр. и доп. – М.: Изд-во МГУ, 2004. – 416 с.
3. Шубин М.А. Лекции об уравнениях математической физики. – М.: МЦНМО, 2001.
4. Владимиров В.С., Жаринов В.В. Уравнения математической физики. – М.: Физматлит 2003.
5. Владимиров В.С., Вашарин А.А. Сборник задач по уравнениям математической физики. – М.: Физматлит, 2001.
6. Голоскоков Д. П. Уравнения математической физики. Решение задач в системе Maple. Учебник для вузов. – СПб.: Питер, 2004. – 544 с.
7. Треногин В.А. Методы математической физики. – М.: РХД 2002.
8. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике. – М.: Физматлит, 2003.
9. Боголюбов А.Н., Кравцов В.В. Задачи по математической физике: Учеб. пособие. – М.: Изд-во МГУ, 1998. – 350 с.
10. Шарма Дж., Сингх К. Уравнения в частных производных для инженеров. – М.: Техносфера, 2002.
11. Мартинсон Л.К., Малов Ю.И. Дифференциальные уравнения математической физики. - МГТУ им. Н.Э. Баумана, 2002. – 368 с.
Приложение №1
Простейшие задачи Штурма – Лиувилля
| № | Задача | Собственные значения | Собственные функции |
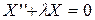 , ,
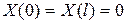
| 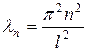 , ,
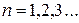
| 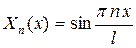
| |
| 2а | 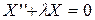 , ,
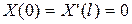
| 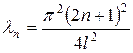 , ,
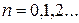
| 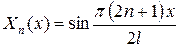
|
| 2б | 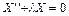 , ,
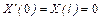
| 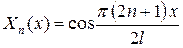
| |
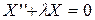 , ,
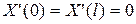
| 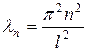 , ,
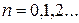
| 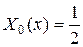
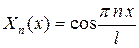 , ,
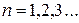
| |
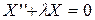 , ,
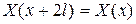 или
или
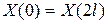 , ,
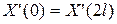
| 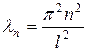 , ,
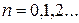
| 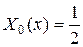
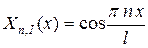 , ,
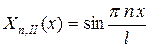 , ,
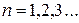
|
Приложение №2
Общий вид ряда Фурье по собственным функциям
| № | Вид разложения | Коэффициенты |
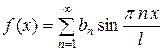 Синус-ряд Фурье
Синус-ряд Фурье
| 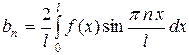
| |
| 2а | 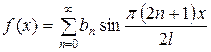
| 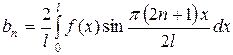
|
| 2б | 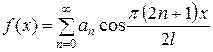
| 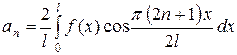
|
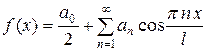 Косинус-ряд Фурье
Косинус-ряд Фурье
| 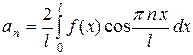 , ,
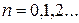
| |
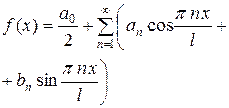 Полный ряд Фурье
Полный ряд Фурье
| 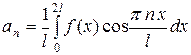 , ,
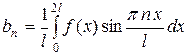 , ,
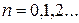
|
Свойства ряда Фурье по собственным функциям
|
|
|
1. 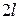 - периодична, нечетна;
- периодична, нечетна;
2а. 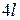 - периодична, нечетна,
- периодична, нечетна, 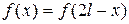 ;
;
2б. 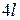 - периодична, четна,
- периодична, четна, 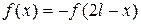 .
.
3. 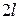 - периодична, четна;
- периодична, четна;
4. 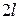 - периодична.
- периодична.
 2015-03-07
2015-03-07 333
333






