Формой платы за кредит выступает ссудный процент – это денежное вознаграждение, которое получают кредиторы, предоставляя кредит. Ссудный процент является ценой кредита или платой, которую заемщик стоимости в денежной или товарной форме должен заплатить кредитору за пользование кредитом. Когда кредитор предоставляет заем, он отсрочивает свое потребление (альтернативное использование денег) на определенный период времени. За отказ от текущего потребления кредитор взимает плату и тем самым увеличивает ожидаемое потребление в будущем.[73] Ставка процента – это отношение процентного дохода к величине ссуды.
Уплата процента – это передача части прибыли, получаемой заемщиком, кредитору. Ее источником является доход, созданный в процессе производительного использования ссудного капитала.
Поскольку ссудный процент – это цена заемных денег, то, как и любая цена, он выполняет функцию распределения денежного и соответственно реального капитала среди различных предприятий и инвестиционных объектов. Согласно этой функции имеющиеся в наличии деньги распределяются между теми заемщиками, степень доходности или ожидаемая норма прибыли которых является достаточно высокой, чтобы гарантировать выплату существующей ставки процента. Процентная ставка, выполняя свою функцию, распределяет реальный капитал между теми отраслями, где он окажется наиболее производительным и соответственно наиболее прибыльным. Таким образом, судный процент – это не пассивный участник кредитной сделки, он оказывает стимулирующее воздействие на функционирование заемных средств, эффективное использование ссужаемой стоимости. Необходимость уплаты процента стимулирует заемщика к получению максимальной прибыли в условиях рыночной конкуренции, чтобы расплатиться с кредитором и иметь средства для расширенного воспроизводства. Если предприятие будет нерационально применять заемные средства (а также и собственные), то цена за кредит (процент за кредит) поглотит всю его прибыль. [74]
Процент важен не только для заемщика, но и для кредитора – банка. В зависимости от того, платит или взимает банк проценты, они делятся на активные и пассивные. Если банк взимает проценты за предоставленные кредиты, он получает активные проценты, которые представляют собой процентный доход. Если банк выплачивает проценты своим клиентам (вкладчикам и кредиторам), то это пассивные проценты, которые составляют процентный расход.
Ставка процента формируется под воздействием множества факторов, таких как:
– степень развития и специфические особенности кредитной системы страны;
– объем денежных накоплений населения;
– уровень развития и состояние экономики;
– размер бюджетного дефицита;
– состояние национальной валюты – чем более устойчива национальная валюта, тем ниже ставка процента;
– государственное регулирование экономики;
– вид и срок кредита;
– репутация (кредитная история) и экономическое положение заемщика.
Факторы, влияющие на уровень ссудного процента, могут быть разделены на внутренние и внешние (рис. 8.7).
Порядок начисления процентов кредитными организациями регулируется Положением ЦБ РФ от 26 июня 1998 г. № 39-П «О порядке начисления процентов по операциям, связанным с привлечением и размещением средств банками, и отражения указанных операций по счетам бухгалтерского учета». При выполнении финансовых операций используются различные схемы и методы начисления процентов.
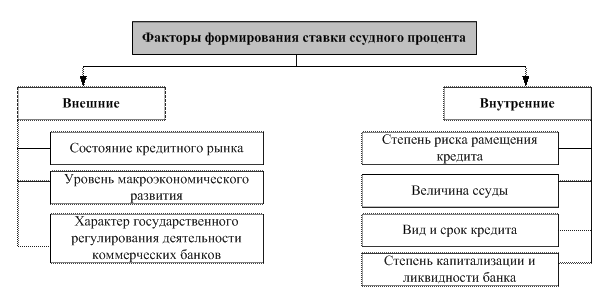
Рис. 8.7. Факторы, влияющие на уровень ставки процента
Депозитные (вкладные) операции коммерческих банков – это операции по привлечению средств юридических и физических лиц во вклады на определенный срок либо до востребования, а также остатков средств на расчетных счетах клиентов для использования их в качестве кредитных ресурсов и в инвестиционной деятельности. При совершении коммерческими банками депозитных операций ссудный процент принимает форму депозитного процента. Ставка депозитного процента устанавливается коммерческими банками по соглашению с клиентами.
Кредитные (ссудные) операции коммерческих банков – это операции по предоставлению денежных средств во временное пользование на условиях срочности и с уплатой процентов.
Дифференциация видов ссудного процента основывается на нескольких критериях:
1) формах кредита: коммерческий, банковский, потребительский и т.д.;
2) видах кредитных учреждений: учетный, банковский, ломбардный;
3) сроках ссуды: по краткосрочным (ставка денежного рынка) и долгосрочным (ставка по облигационным займам);
4) видах кредита: по ссудам в оборотные активы, по овердрафтному кредиту, по учету векселей, по целевым ссудам и т.д.;
5) видах операций: по ссудам юридическим и физическим лицам, по межбанковским кредитам;
6) способах начисления процентов: простые и сложные.
Простые проценты – это метод расчета дохода кредитора от предоставления денежных ресурсов в долг заемщику, при котором проценты начисляются на одну и ту же величину капитала в течение всего срока ссуды.
Расчет суммы ссуды с процентами (наращение) осуществляется по формуле 8.1.
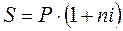 , (8.1)
, (8.1)
где 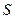 – наращенная сумма;
– наращенная сумма;
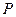 – сумма ссуды;
– сумма ссуды;
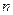 – срок ссуды (число лет);
– срок ссуды (число лет);
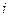 – годовая процентная ставка.
– годовая процентная ставка.
Расчет суммы процентов по ссуде производится по формуле 8.2.
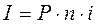 (8.2)
(8.2)
Пример 1. В сберегательном банке открыт инвестиционный вклад в сумме 300 тыс. руб. с начислением процентов по ставке 10,7% годовых. Общий срок хранения денежных средств составил 2 года. Определить сумму вклада с процентами, которую получил инвестор при закрытии счета, и сумму накопленных процентов.
Решение. Сумму вклада с процентами определим по формуле 8.1.
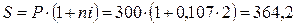
Сумма вклада с процентами составит 364,2 тыс. руб. Сумму накопленных процентов определим по формуле 10.2.
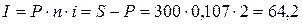
Сумма накопленных процентов – 64,2 тыс. руб.
Если срок, на который деньги предоставляется в долг, задан в днях (составляет менее года или неполное число лет), то для наращения используется формула 8.3.
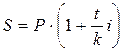 , (8.3)
, (8.3)
где 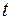 – срок кредита в днях;
– срок кредита в днях;
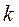 – расчетное количество дней в году. В случае использования точных процентов
– расчетное количество дней в году. В случае использования точных процентов 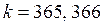 . В расчете обыкновенных (коммерческих) процентов
. В расчете обыкновенных (коммерческих) процентов 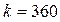 .
.
В мировой банковской практике в зависимости от способа исчисления срока ссуды 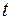 и расчетной длительности года
и расчетной длительности года 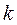 выделяют три метода расчетов процентов и наращенной суммы:
выделяют три метода расчетов процентов и наращенной суммы:
а) обыкновенные проценты с приблизительным числом дней ссуды (из расчета каждый месяц – 30 дней) и 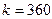 – германский метод;
– германский метод;
б) обыкновенные проценты с точным числом дней ссуды и 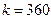 – французский метод;
– французский метод;
в) точные проценты с точным числом дней ссуды и 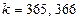 – английский метод.
– английский метод.
В российской банковской практике в соответствии с положением ЦБ РФ от 26.06.1998 «О порядке начисления процентов по операциям, связанным с привлечением и размещением денежных средств, и отражении этих операций по счетам бухгалтерского учета» коммерческим банкам рекомендовано использовать точные проценты.
Пример 2. Вкладчик внес вклад в банк в сумме 15600 руб. под 8% годовых. Срок вклада с 16.05. по 27.09. Определите сумму вклада на конец срока, используя германский и английский метод.
Решение.
а) Определим накопленную сумму германским методом по формуле 8.3, при этом 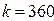 дней, а
дней, а 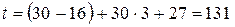 день.
день.
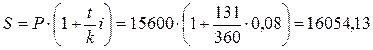 .
.
Накопленная сумма с процентами составит 16054,13 руб.
б) Определим накопленную сумму английским методом по формуле 10.3, при этом 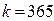 дней, а
дней, а 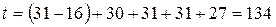 дня.
дня.
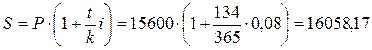 .
.
Накопленная сумма с процентами составит 16058,17 руб.
Учет инфляции при расчете процентов. В условиях инфляции расчет процентов осуществляется с корректировкой процентной ставки на уровень инфляции, показывающий темпы прироста цен в экономике (8.4):
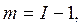 (8.4)
(8.4)
где 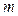 – уровень инфляции в десятичном выражении;
– уровень инфляции в десятичном выражении;
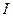 – индекс инфляции в десятичном выражении.
– индекс инфляции в десятичном выражении.
Номинальная ставка, скорректированная на уровень инфляции (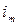 ), определяется по формуле 8.5.
), определяется по формуле 8.5.
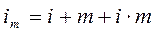 (8.5)
(8.5)
Пример 3. Вкладчик внес вклад в банк в сумме 3500 руб. под 5% годовых (без учета инфляции). Ожидаемый годовой уровень инфляции – 6%. Срок вклада с 6.06. по 17.09. Определите сумму вклада на конец срока, используя точные проценты. Процентную ставку необходимо скорректировать на уровень инфляции.
Решение. Определим процентную ставку, скорректированную на уровень инфляции по формуле 10.5.
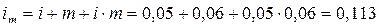 .
.
Рассчитаем срок, за который будут начислены проценты, используя точное число дней (английский метод).
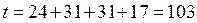 .
.
Определим сумму вклада с процентами по формуле 10.3.
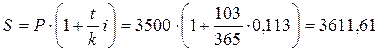 .
.
Сумма вклада с процентами составит 3611,61 руб.
Расчет процентов при изменяющемся остатке денежных средств на счете. [75] В депозитной практике банков сумма на счетах клиентов часто меняется, что связано с поступлением или изъятием денежных средств. Для определения суммы начисленных процентов за срок хранения денег при изменяющемся остатке используются процентное число (8.6) и дивизор или процентный ключ(8.7).
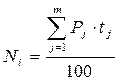 , (8.6)
, (8.6)
где 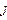 – порядковый номер периода хранения определенной суммы денежный средств;
– порядковый номер периода хранения определенной суммы денежный средств;
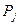 – сумма денежных средств на счете в течение
– сумма денежных средств на счете в течение 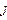 -того периода;
-того периода;
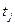 – продолжительность
– продолжительность 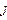 -того периода в днях.
-того периода в днях.
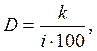 (8.7)
(8.7)
где 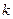 – расчетное количество дней в году;
– расчетное количество дней в году;
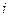 – годовая процентная ставка.
– годовая процентная ставка.
Сумма начисленных процентов определяется по формуле 8.8.
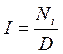 (8.8)
(8.8)
Пример 4. При открытии вклада по ставке 9% годовых на счет 1.09. была внесена сумма 200 тыс. руб. Затем на счет 5.11. была добавлена сумма 40 тыс. руб., 10.12.со счета снята сумма 135 тыс. руб., а 29.12. счет был закрыт. Определите общую сумму, полученную вкладчиком при закрытии счета.
Решение. Рассчитаем процентное число по формуле 8.6.
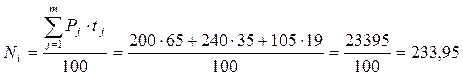
Определим дивизор по формуле 10.7.
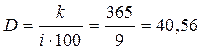 .
.
Рассчитаем сумму накопленных за общий срок вклада процентов по формуле 8.8.
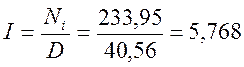 .
.
Сумма процентов составила 5,768 тыс. руб. Рассчитаем общую сумму денежных средств, которую получит вкладчик при закрытии счета 29.12.
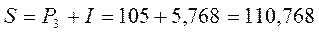 .
.
Сумма, которую получил вкладчик при закрытии счета, составила 110,768 тыс. руб.
Сложные проценты – это способ начисления процентных платежей при начислении процентов не только на первоначальную сумму, но и на сумму начисленных процентов.
Используются два способа начисления сложных процентов: антисипативный и декурсивный.
При антисипативном методе проценты начисляются в начале расчетного периода. Этот метод, как правило, применяется в условиях высокой инфляции и позволяет определить, на какую сумму возрастет первоначальный капитал, если вычисление сложных процентов производится по ставке 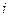 . Расчет суммы с процентами при антисипативном методе осуществляется по формуле 8.9.
. Расчет суммы с процентами при антисипативном методе осуществляется по формуле 8.9.
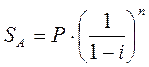 , (8.9)
, (8.9)
где 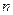 – срок ссуды (число лет).
– срок ссуды (число лет).
Если срок ссуды составляет менее года, то используется формула 10.10.
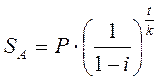 (8.10)
(8.10)
При расчете антисипативным методом накапливается больший доход, чем при декурсивном методе начисления сложных процентов.
Декурсивный метод основан на начислении процентов в конце расчетного периода. Если проценты начисляются один раз в год, для расчета наращенной суммы используется формула 8.11.
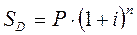 (8.11)
(8.11)
Если период начисления меньше года, используется формула 8.12.
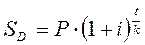 (8.12)
(8.12)
Пример 5. Вклад в сумме 5600 руб. открыт в банке под 11% годовых на срок 6 лет. Определите доход от инвестирования денежных средств при начислении сложных процентов декурсивным и антисипативным методами.
Решение.
а) Для расчета наращенной суммы антисипативным методом воспользуемся формулой 8.9.
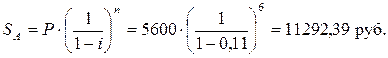
Сумма процентов составит:
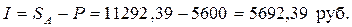
б) Для расчета наращенной суммы декурсивным методом воспользуемся формулой 8.11.
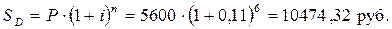
Сумма процентов составит:
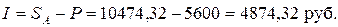
Дисконтирование. В финансовой практике зачастую возникает задача, обратная определению наращенной суммы, т.е. по заданной сумме 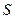 , относящейся к будущему моменту времени, необходимо определить ее текущий (на настоящий момент времени) денежный эквивалент. Эта задача возникает, например, при удержании процентов на ссуду непосредственно при ее выдаче. В этом случае сумма
, относящейся к будущему моменту времени, необходимо определить ее текущий (на настоящий момент времени) денежный эквивалент. Эта задача возникает, например, при удержании процентов на ссуду непосредственно при ее выдаче. В этом случае сумма 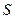 дисконтируется, а разность
дисконтируется, а разность 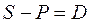 называют дисконтом. Также дисконтирование применяется при оценке денежных потоков с учетом фактора времени в задачах финансового менеджмента.
называют дисконтом. Также дисконтирование применяется при оценке денежных потоков с учетом фактора времени в задачах финансового менеджмента.
Применение дисконтирование основано на объективно существующей временной неравноценности денег, которая означает, что одна и та же сумма, полученная сегодня, более ценна, чем полученная спустя некоторое время, вследствие того, что полученные раньше деньги можно инвестировать под проценты и получить дополнительный доход. В финансовом планировании с помощью дисконтирования плановые суммы приводятся в сопоставимый вид по фактору времени.
В зависимости от вида ставки (процентной или учетной) различают два вида дисконтирования: математическое и коммерческое.
Математическое дисконтирование – это дисконтирование, при котором ставкой дисконтирования обычная процентная ставка (ставка процентов). Математическое дисконтирование может осуществляться по простой процентной ставке (8.13) и по сложной процентной ставке (8.14).
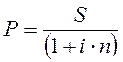 , (8.13)
, (8.13)
где 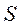 – «будущая» денежная сумма;
– «будущая» денежная сумма;
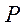 – текущий эквивалент «будущей» денежной суммы;
– текущий эквивалент «будущей» денежной суммы;
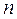 – срок ссуды (число лет);
– срок ссуды (число лет);
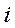 – годовая простая процентная ставка.
– годовая простая процентная ставка.
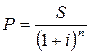 , (8.14)
, (8.14)
где 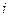 – годовая сложная процентная ставка.
– годовая сложная процентная ставка.
Коммерческое (банковское) дисконтирование связано с расчетом дисконта, т.е. скидки от первоначальной суммы. В расчетах ставкой дисконтирования выступает учетная ставка. Коммерческое дисконтирование, также как и математическое, может осуществляться по простой учетной ставке (8.15) и по сложной учетной ставке (8.16).
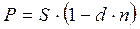 (8.15)
(8.15)
где 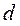 – учетная ставка.
– учетная ставка.
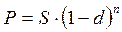 (8.16)
(8.16)
Пример 6. Какую сумму необходимо внести в банк на депозит, чтобы по окончании срока депозита сумма составила 344000 руб.? Срок депозита пять лет. В расчетах используется математическое дисконтирование по сложной процентной ставке – 10% годовых.
Решение. Для расчета используем формулу математического дисконтирования по сложной процентной ставке (8.14).
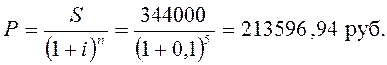
Пример 7. В банк для учета представлен вексель. Вексельная сумма 75 тыс. руб. Срок до даты погашения векселя 34 дня. Простая учетная ставка по операциям банка составляет 28% годовых. Определить сумму, которую выплатит банк в результате учета векселя и размер дисконта в пользу банка.
Решение. Для расчета используем формулу коммерческого дисконтирования по простой учетной ставке (8.15). Так как период инвестирования составляет менее года то вместо значения 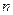 подставим в формулу выражение
подставим в формулу выражение 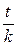
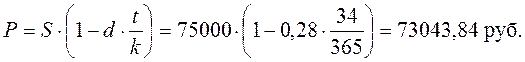
Векселедержатель получит от банка за учтенный вексель 73043,84 руб. Доход банка от операции учета векселя (дисконт) составит:
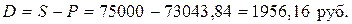
 2015-03-08
2015-03-08 3570
3570
