Для плоскопараллельного движения

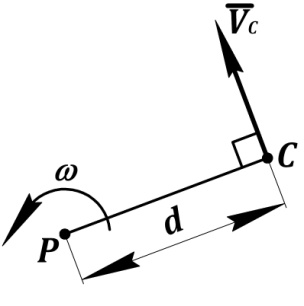
Рис. 69. Кинетическая энергии механической системы

при плоскопараллельном движении

Точка 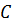– центр масс, 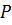– полюс (рис. 69).

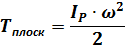
Момент инерции 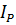– переменная величина, так как положение точки 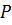меняется. Постоянной является величина 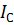. По теореме Гюйгенса-Штейнера

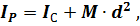
где .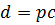

Тогда с учётом, что относительно полюса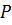

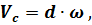
получаем

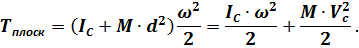
14. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МЕХАНИЧЕСКОЙ СИСТЕМЫ

Важное обстоятельство: в отличие от предыдущих теорем здесь (для МС) внутренние силы не исключаются.

Реальный пример: работа сил давления пороховых газов в системе «снаряд – откатывающиеся части» в орудии. Эти внутренние силы сообщают скорости телам системы.

Для всех 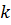точек системы в дифференциальной форме элементарное изменение кинетической энергии

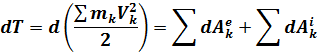
– сумма элементарных работ внешних и внутренних сил.

После интегрирования в пределах перемещения системы из положения 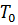в положение 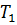получим

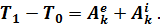
Частные случаи, когда всё же :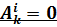

1) неизменная система, в которой расстояние между каждыми двумя точками неизменно;

2) система с идеальными связями, в частности шарнирное соединение: если пренебречь силой трения в шарнире (а это и есть идеальная связь), то работа реакции шарнира равна нолю.

Также не изменяют величину 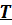силы трения о неподвижную поверхность при качении без проскальзывания.