Анализ рядов динамики

Изучение изменения различных явлений во времени — одна из важнейших задач статистики. Решается эта задача путем составления и анализа рядов динамики (иногда их также называют временными или хронологическими рядами).

Ряд динамики представляет собой числовые значения опреде­ленного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).

Числовые значения того или иного статистического показателя, составляющие ряд динамики, называют уровнями ряда и обычно обозначают через у. Первый член ряда у₀ (или у₁) называют начальным уровнем, а последний у_n — конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t. Ряды динамики представляют в виде таблицы или графически.

В статистике различают моментные и интервальные ряды динамики.

Моментным называется ряд, уровни которого характеризуют значение показателя (явления) по состоянию на определенные моменты времени (дату).

Пример. Государственный внешний долг Российской федерации:

Дата	1.01.1999	1.01.2000	1.01.2001	1.01.2002	1.01.2003	1.01.2004
Гос. долг, млрд. долл. США	156,7	158,4	142,4	130,1	122,1	119,1

Интервальным называется ряд, уровни которого характеризуют значение показателя, достигнутое за определенный период времени (интервал).

Пример. Валовый внутренний продукт в России:

Год
ВВП, тыс. руб.	4823233,5	7305646,3	9039440,6	10863361,6

Отличительная особенность интервальных рядов: их уровни можно дробить и складывать (суммировать). Например, зная добычу угля по годам, можно разделить каждый уровень на 12 и получить новые данные – о среднемесячной добыче угля за указанный период. Или же, суммируя данные о численности родившихся по месяцам, можно получить численность родившихся за год. Подобные действия в уровнями моментного ряда не имеют смысла.

Одно из требований, которые предъявляются к анализируемым рядам динамики – сопоставимость уровней ряда. Если данные несопоставимы, то исходя из цели исследования, необходимо повести дополнительные расчеты. Для сопоставимости должна быть обеспечена одинаковая полнота охвата различных частей явления (например, при характеристики численности студентов нельзя в одни годы учитывать только дневное отделение, а в другие еще и заочное) и одинаковость границ территории (например, при изучении темпов экономического развития целесообразно использовать ежегодно данные по территории в одних и тех же границах).

Одна из первых задач изучения рядов динамики — выявить основную тенденцию (закономерность) в изменении уровней ряда, именуемую трендом. Закономерность в изменении уровней ряда в одних случаях проявляется довольно наглядно, в других — может затушевываться колебаниями, вызванными случайными и неслу­чайными причинами.

При изучении рядов динамики перед статистикой стоят следующие задачи:

- охарактеризовать интенсивность развития явления от периода к периоду;

- охарактеризовать среднюю интенсивность развития за исследуемый период;

- выявить основную тенденцию в развитии явления;

- осуществить прогноз развития на будущее;

- изучить сезонные колебания.

Показатели ряда динамики:

Анализ рядов динамики начинается с определения того, как именно изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении.

Чтобы проследить за направлением и размером изменений уровней во времени, для рядов динамики рассчитывают такие показатели, как:

- абсолютные приросты (изменения) уровней;

- темпы роста;

- темпы прироста (снижения) уровней;

Абсолютный прирост (абсолютное изменение) уровней рассчитывается как разность между двумя уровнями ряда. Он показывает, на сколько (в единицах измерения показателей ряда) уровень одного периода больше или меньше уровня какого-либо предшествующего периода, и, следовательно, может иметь знак «+» (при увеличении уровней) или «—» (при уменьшении уровней).

В зависимости от базы сравнения абсолютные приросты могут рассчитываться как цепные и как базисные.

Вычитая из каждого уровня предыдущий (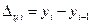), получаем абсолютные изменения уровней ряда за отдельные периоды как цепные. Вычитая из каждого уровня начальный 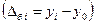получаем накопленные итоги прироста (изменения) показателя с начала изучаемого периода, т.е. абсолютные изменения рассчитываются как базисные.

Если значения цепных абсолютных изменений постоянны, то уровни ряда изменяются равномерно. Если же абсолютные приро­сты от периода к периоду возрастают (или убывают), то уровни изменяются ускоренно (или замедленно).

Наряду с абсолютными изменениями уровней ряда важно измерить также их относительное изменение.

Темп роста — относительный показатель, рас­считываемый как отношение двух уровней ряда.

В зависимости от базы сравнения темпы роста могут рассчиты­ваться как цепные, когда каждый уровень сопоставляется с уровнем предыдущего периода 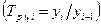и как базисные, когда все уровни сопоставляются с уровнем одного какого-то периода, принятого за базу сравнения, часто это начальный уровень ряда: 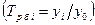. Соответственно, цепные темпы роста характеризуют интенсивность изменения в каждом отдельном периоде, а базисные — за отрезок времени, отделяющий данный уровень от базисного.

Темпы роста как относительные величины могут выражаться в виде коэффициентов, т.е. простого кратного отношения (если база сравнения принимается за единицу), и в процентах (если база сравнения принимается за 100 единиц). Говоря о темпах, чаще всего имеют в виду отношение уровней в процентах.

Выраженные в коэффициентах темпы роста показывают, во сколько раз уровень данного периода больше уровня базы сравнения или какую часть его составляет. При процентном выраже­нии темп роста показывает, сколько процентов составляет уровень данного периода по сравнению с уровнем базы сравнения.

Между цепными и базисными коэффициентами роста существует связь, позволяющая при необходимости переходить от цепных к базисным и наоборот.

В частности:

- произведение цепных коэффициентов роста равно базисному;

- результат деления двух базисных коэффициентов равен цепному (промежуточному).

Темп прироста — относительный показатель, показывающий, на сколько процентов данный уровень больше (или меньше) другого, принимаемого за базу сравнения.

Этот показатель можно рассчитать двумя способами:

- путем вычитания 100% из темпа роста (снижения), т.е. ;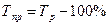

- как процентное отношение абсолютного прироста к тому уровню, по сравнению с которым рассчитан абсолютный прирост, т. е. 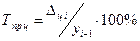или .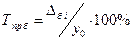

Иногда для анализа рассчитывается такой показатель, как абсолютное значение 1% прироста — отношение абсолютного прироста уровня к темпу прироста (за соответствующий период):

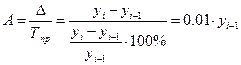
Абсолютное значение 1 % прироста равно одной сотой предыдущего уровня.

Для базисных абсолютных приростов и темпов прироста расчет А не имеет смысла, так как при сравнении всех накопленных приростов с одним и тем же первоначальным уровнем у₀ для всех периодов будет получаться одно и то же значение 1 % прироста.

Для характеристики интенсивности развития за длительный период рассчитываются средние показатели рядов динамики.

Обобщенной характеристикой динамического ряда может служить прежде всего средний уровень ряда у. Поскольку средняя вели­чина в данном случае рассчитывается из меняющихся во времени показателей, то она называется средней хронологической.

Для разных видов рядов динамики средний уровень рассчитывается неодинаково.

В интервальном ряду абсолютных величин с равными периодами (интервалами) средний уровень рассчитывается как средняя арифметическая простая из уровней ряда:

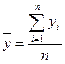
где y_i — отдельные уровни ряда; n – число уровней.

Для моментного ряда, содержащего n уровней с равными промежутками между датами (моментами), средний уровень определяется по формуле:

.

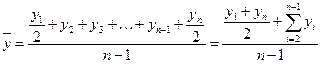Пример. По данным Государственного внешнего долга Российской федерации рассчитать средний уровень ряда:

Дата	1.01.1999	1.01.2000	1.01.2001	1.01.2002	1.01.2003	1.01.2004
Гос. долг, млрд. долл. США	156,7	158,4	142,4	130,1	122,1	119,1

,

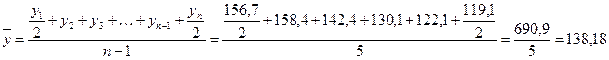то есть в среднем за рассматриваемый промежуток времени государственный внешний долг составил 138,18 млрд. долл.

Средний абсолютный прирост (изменение) уровней рассчитывается как средняя арифметическая простая из отдельных цепных приростов или на основе накопленного абсолютного прироста за n периодов:

.

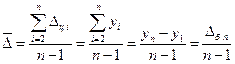Средний темп роста рассчитывается как средняя геометрическая из цепных темпов роста:

.

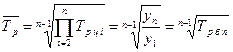Средний темп прироста рассчитываются на основе средних темпов роста путем вычитания из последних 100%:

.

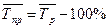Методы выявления основной тенденции (тренда) в рядах динамики

Уровни ряда динамики формируются под влиянием взаимодействия многих факторов, одни из которых, будучи основными, главными, определяют закономерность, тенденцию развития, другие — случайные — вызывают колебания уровней. Изучая ряды динамики, пытаются разделить эти компоненты и выявить основную закономерность развития явления в отдельные периоды, т.е. выявить общую тенденцию в изменении уровней рядов, освобожденную от действия случайных факторов. С этой целью (устранить колебания, вызванные случайными причинами) ряды динамики подвергают обработке.

Существует несколько методов обработки рядов динамики: метод укрупнения интервалов, метод скользящей средней и аналитическое выравнивание. Во всех методах вместо фактических уровней при обработке ряда рассчитываются иные (расчетные) уровни, в которых взаимопогашается действие случайных факторов и тем самым уменьшается колеблемость уровней. Уровни в результате становятся как бы «выравненными», «сглаженными» по отношению к исходным фактическим данным. Такие методы обработки рядов называются сглаживанием или выравниванием рядов динамики.

Метод укрупнения интервалов.

Простейший метод сглаживания уровней ряда — укрупнение интерваловвремени, для которых определяется итоговое значение или средняя величина исследуемого показателя. Этот метод особенно эффективен, если первоначальные уровни ряда относятся к коротким промежуткам времени. Например, если имеются данные о ежесуточной погрузке грузов по какой-либо железной дороге за месяц, то в таком ряду возможны значительные колебания уровней, так как чем меньше период, за который приво­дятся данные, тем больше влияние случайных факторов.

Чтобы устранить это влияние, рекомендуется укрупнить интервалы времени, например до 5 или 10 дней, и для этих укрупненных интервалов рассчитать общий или среднесуточный объем погрузок (соответственно по пятидневкам или декадам). В ряду с укрупнен­ными интервалами времени закономерность изменения уровней будет более наглядной.

Метод скользящей средней.

В данном случае фактические уровни заменяются средними уровнями, рассчитанными для последовательно подвижных (скользящих) укрупненных интервалов, охватыва­ющих т уровней ряда.

Например, если принять т = 3, то сначала рассчитывается средняя величина из первых трех уровней, затем находится средняя величина из второго, третьего и четвертого уровней, потом из тре­тьего, четвертого и пятого и т.д., т.е. каждый раз в сумме трех уровней появляется один новый уровень, а два остаются прежними. Это и обусловливает взаимопогашение случайных колебаний в средних уровнях. Рассчитанные из т членов скользящие средние относятся к середине (центру) каждого рассматриваемого интервала.

Сглаживание методом скользящей средней можно проводить по любому числу членов т, но удобнее, если т — нечетное число, так как в этом случае скользящая средняя сразу относится к конкретной временной точке — середине (центру) интервала. Недостатком метода скользящей средней является то, что сглаженный ряд «укорачивается» по сравнению с фактическим с двух концов: при нечетном т на 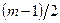с каждого конца, а при четном — на т/2 с каждого конца. Этот метод сглаживает (устраняет) лишь случайные колебания. Если же, например, ряд содержит сезонную волну, она сохранится и после сглаживания.

Метод скользящей средней и укрупнения интервалов являются механическими, эмпирическими и не позволяют выразить общую тенденцию изменения уровней в виде математической модели.

Аналитическое выравнивание.

Более совершенный метод обработки рядов динамики в целях устранения случайных колебаний и выявления тренда. Суть аналитического выравнивания заключается в замене эмпирических (фактических) уровней y_i теоретическими 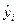,которые рассчитаны по определенному уравнению, принятому за математическую модель тренда, где теоретические уровни рассматриваются как функция времени: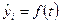

Задача аналитического выравнивания сводится к следующему:

- определение на основе фактических данных вида (формы) гипотетической функции 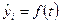способной наиболее адекватно отразить тенденцию развития исследуемого показателя;

- нахождение по эмпирическим данным параметров указанной функции (уравнения);

- расчет по найденному уравнению теоретических (выравненных) уровней.

Виды функций, с помощью которых можно описать поведение рядов динамики были рассмотрены в теме «Изучение корреляционных взаимосвязей». Выбор той или иной функции для выравнивания ряда динамики осуществляется, как правило, на основании графического изображения эмпирических данных, дополняемого содержательным анализом особенностей развития исследуемого показателя (явления) и специфики разных функций. Определенную вспомогательную роль при выборе аналитической функции играют также механические приемы сглаживания (укрупнение интервалов и метод скользящей средней).

Частично устраняя случайные колебания, они помогают более точно определить тренд и выбрать адекватную модель (уравнение) для аналитического выравнивания. Кроме того, существуют некоторые условия, которыми полезно руководствоваться при выборе функции. Так, например, выравнивание по прямой линии (линейной функции) y_t = а₀ + a₁ t эффективно для рядов, уровни которых изменяются примерно в арифметической прогрессии, т.е. когда первые разности уровней (абсолютные приросты более или менее постоянны.

Параметры искомых уравнений при аналитическом выравнивании могут быть определены по-разному. Чаще всего их определяют, решая систему уравнений, полученных методом наименьших квадратов.

Выравнивание по линейной функции y_t = а₀ + a₁ t.

Способ получения параметров этого уравнения был рассмотрен выше. Но для рядов динамики расчеты можно упростить, если отсчет времени вести от середины ряда. Например, при нечетном числе уровней серединная точка (год, месяц) принимается за ноль, тогда предшествующие периоды обозначаются соответственно -1, -2, -3, и т. д., а следующие за средним – соответственно +1, -2, -3 и т. д. При четном числе уровней два серединных момента (периода) времени обозначаются -1 и +1, а все последующие и предыдущие, соответственно через два интервала: 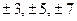и т. д.

При таком порядке отсчета времени 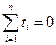. Поэтому система уравнений упрощается до двух уравнений, каждое их которых решается самостоятельно:

.

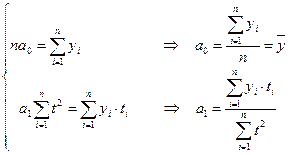Изучая и анализируя ряды динамики, стремятся на основе выявленных особенностей изменения явлений в прошлом предугадать поведение рядов в будущем, т.е построить различные прогнозы путем экстраполяции (продления) рядов.

Экстраполяцию ряда динамики можно осуществить различными способами. Однако независимо от применяемого способа экстраполяции обязательно предполагается, что закономерность (тенденция) изменения, выявленная для определенного периода в прошлом, сохранится на ограниченном отрезке времени в будущем.

Поэтому любому прогнозированию в виде экстраполяции ряда должно предшествовать тщательное изучение длительных рядов динамики, которое позволило бы определять тенденцию изменения. Поскольку тенденция развития также может изменяться, то данные, полученные путем экстраполяции ряда, надо рассматривать как вероятностные, то есть своего рода оценки.

Приемы экстраполяции рядов динамики, помогающие прогнозировать те или иные показатели:

1. Если при анализе ряда динамики обнаруживается, что абсолютные приросты уровней примерно постоянны, можно рассчитать средний абсолютный прирост (как среднюю арифметическую) и последовательно прибавить его к последнему уровню ряда столько раз, на сколько периодов экстраполируется ряд.

2. Если за исследуемый ряд лет (или другие периоды) годовые коэффициенты роста остаются более-менее постоянными, можно рассчитать средний коэффициент роста и умножить последний уровень ряда на средний коэффициент роста в степени, соответствующей периоду экстраполяции.

3. Учитывая, что между изменениями нескольких показателей существует зависимость, можно экстраполировать один ряд динамики на основе сведений об изменении второго ряда, связанного с ним. Например, определив зависимость между изменением объема капитальных вложений и объемом выпускаемой продукции в, можно экстраполировать данные о производстве продукции на основе данных о намеченных капиталовложениях;

4. Можно экстраполировать ряды на основе выравнивания их по определенной аналитической формуле. Зная уравнение для теоретических уровней, и подставляя в него значения t за пределами исследованного ряда, можно рассчитать для данных t вероятностные уровни y_i. Этот метод можно использовать, только если сумма фактических уровней ряда отличается от суммы теоретических значений не более чем на 5%.

Экономическое прогнозирование невозможно без хорошего знания изучаемого явления и владения различными методами обработки динамических рядов, которые в каждом отдельном случае помогли бы обнаружить общую закономерность изменения, периодичность в повышении или снижении уровней (если она имеет место), случайные колебания и корреляцию между отдельными рядами.

Пример. Построить динамический ряд, используя 12 и более уровней. Проанализировать, используя аналитические и средние показатели. Провести выравнивание, используя метод скользящей средней и аналитическое выравнивание. На основе полученного уравнения проэкстраполировать уровни ряда динамики на 2-3 уровня вперед.

Рассмотрим данные о вводе в действие жилых домов (тыс. кв. м.) за 2009 год. То есть ряд является интервальным. В 1-ую расчетную таблицу внесем исходные данные и аналитические показатели заданного ряда динамики.

Таблица 6. Расчетная таблица аналитических показателей ряда динамики.

№	Месяц	уровень ряда	Абсолют.	прирост	Темп	роста	Темп	прироста	Абсолсодер. 1% при-роста
t		у	цепной	базисный	цепной	базисный	цепной	базисный	А
	янв	3,358
	фев	12,003	8,645	8,645	357,44%	357,44%	257,44%	257,44%	0,034
	март	14,232	2,229	10,874	118,57%	423,82%	18,57%	323,82%	0,120
	апр	13,767	-0,465	10,409	96,73%	409,98%	-3,27%	309,98%	0,142
	май	10,72	-3,047	7,362	77,87%	319,24%	-22,13%	219,24%	0,138
	июнь	8,882	-1,838	5,524	82,85%	264,50%	-17,15%	164,50%	0,107
	июль	3,981	-4,901	0,623	44,82%	118,55%	-55,18%	18,55%	0,089
	авг	16,05	12,069	12,692	403,17%	477,96%	303,17%	377,96%	0,040
	сент	15,17	-0,88	11,812	94,52%	451,76%	-5,48%	351,76%	0,161
	окт	11,606	-3,564	8,248	76,51%	345,62%	-23,49%	245,62%	0,152
	нояб	9,936	-1,67	6,578	85,61%	295,89%	-14,39%	195,89%	0,116
	дек	20,534	10,598	17,176	206,66%	611,49%	106,66%	511,49%	0,099
Итого		140,239	17,176

Уровни ряда и его аналитические показатели варьируют, и возникает необходимость в исчислении средних показателей:

Средний уровень ряда 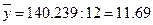тыс. кв. м. То есть в среднем в месяц в 2009 году строилось 11,69 тыс. кв. м. жилой площади.

Средний абсолютный прирост 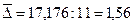тыс. кв. м. То есть в среднем за месяц площадь строящегося жилья увеличивалась на 1,56 тыс. кв. м.

Средний темп роста 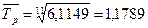, то есть в среднем в месяц застраиваемая площадь увеличивалась в 1,18 раз.

Средний темп прироста 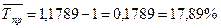, то есть в среднем в месяц застраиваемая площадь увеличивалась на 17,89%.

Проведем выравнивание методом скользящей средней, взяв по 3 уровня ряда, и аналитическое выравнивание. Вычисления сведем во 2-ую расчетную таблицу.

Таблица 7. Выравнивание методом скользящих средних и аналитическое выравнивание.

‹/tr>

Месяц	уровень ряда y	Трехчленные скользящие суммы	трехчленные скользящие средние	ti	ti2	ti*yi	Теоретический уровень ряда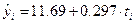
янв	3,358			-11		-36,938	8,416
фев	12,003	29,593	9,864	-9		-108,027	9,011
март	14,232	40,002	13,334	-7		-99,624	9,606
апр	13,767	38,719	12,906	-5		-68,835	10,200
май	10,72	33,369	11,123	-3		-32,16	10,795
июнь	8,882	23,583	7,861	-1		-8,882	11,389
июль	3,981	28,913	9,638			3,981	11,984
авг	16,05	35,201	11,734			48,15	12,579
сент	15,17	42,826	14,275			75,85	13,173
окт	11,606	36,712	12,237			81,242	13,768
нояб	9,936	42,076	14,025			89,424	14,362
дек	20,534					225,874	14,957
Итого	140,239					170,055	140,239

Аналитическое выравнивание проведем по прямой: y_t = а₀ + a₁ t.

Параметры уравнения для приведенных данных равны:

.

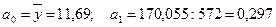То есть уравнение прямой, представляющее собой трендовую модель искомой функции: 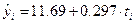. Подставляя в полученное уравнение последовательно значения t, находим выравненные уровни ряда динамики (последняя колонка в таблице).

Так как сумма фактических уровней ряда равна сумме теоретических значений, можно сделать прогноз о строительстве жилой площади на январь, февраль и март 2009 года:

январь = 11,69 + 0,279 * 13 = 15,317 тыс. кв. м.

февраль = 11,69 + 0,279 * 15 = 15,875 тыс. кв. м.

март = 11,69 + 0,279 * 17 = 16,433 тыс. кв. м.

На рис. 4 изображены данные исходного ряда, ряд, выравненный методом скользящей средней и ряд, выравненный по прямой линии (аналитическое выравнивание).

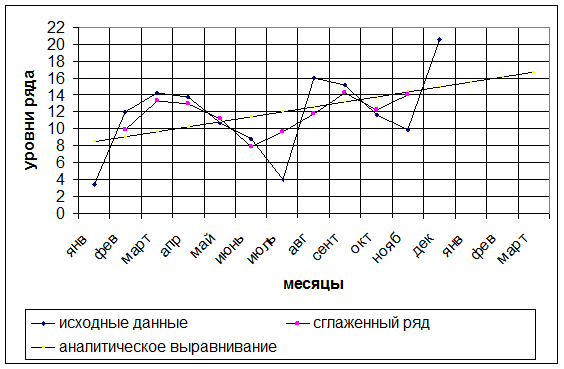
Рис. 4. Графическое представление данных интервального ряда и результатов выравнивания.

Контрольные вопросы

1. Понятие ряда динамики. Моментные и интервальные ряды.
2. Показатели ряда динамики и методы их расчета.
3. Методы выравнивания рядов динамики: метод укрупнения интервалов и метод скользящей средней.
4. Аналитическое выравнивание по линейной функции.
5. Экстраполяция (прогнозирование) на основе уравнения регрессии.