Ряды динамики как основной источник прогнозирования в экономике. Понятие и классификация рядов динамики. Сопоставимость уровней и смыкание рядов динамики. Показатели динамики, их дифференциация.
Упрощенные приемы прогнозирования. Выявление основной тенденции динамики. Общая характеристика методов прогнозирования.
Прогнозирование на основе рядов динамики.
Одной из важнейших задач статистики является изучение развития процессов и явлений во времени. Это осуществляется с помощью построения и анализа статистических рядов динамики.
Ряд динамики - это последовательность одноименных показателей, расположенных в хронологическом порядке. Ряд динамики характеризуется двумя параметрами: показателем, называемым уровнем ряда у; датой и периодом, к которым относится показатель.
Уровни рядов динамики отображают количественную оценку развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными, или средними величинами.
В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим ряды динамики подразделяются на моментные и интервальные.
Моментные ряды динамики отображают состояния изучаемых явлений на определенные даты (моменты) времени. Интервальные ряды динамики отображают итоги развития изучаемых явлений за отдельные периоды (интервалы) времени. Периодом может быть день, неделя, месяц, год.
Для количественной оценки динамики социально-экономических явлений применяются абсолютные и относительные статистические показатели. В основе расчета показателей рядов динамики лежит сравнение его уровней. Если сравнение идет с одним и тем же первым (базисным) уровнем, то вычисляемый показатель называется базисным. Если сравниваются два соседних уровня (каждый последующий уровень ряда сравнивается с предыдущим), вычисляемый показатель называется цепным.
Для выражения изменений уровней рядов динамики в абсолютных величинах вычисляют статистический показатель абсолютного прироста 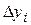 . Величина этого показателя определяется как разность между уровнем изучаемого периода и уровнем, принимаемым за базу сравнения.
. Величина этого показателя определяется как разность между уровнем изучаемого периода и уровнем, принимаемым за базу сравнения.
При определении базисных абсолютных приростов 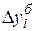 за базу сравнения принимается постоянный уровень.
за базу сравнения принимается постоянный уровень.
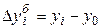 .
.
При определении цепных абсолютных приростов 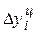 базой сравнения каждый раз выступает уровень предыдущего периода.
базой сравнения каждый раз выступает уровень предыдущего периода.
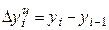 .
.
Абсолютный прирост показывает на сколько единиц текущий уровень больше или меньше предыдущего (базисного).
Между базисными и цепными абсолютными приростами существует связь: сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего периода ряда динамики.
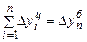 .
.
Распространенным статистическим показателем динамики является темп роста (коэффициент роста).
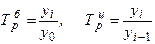 .
.
Темп роста показывает во сколько раз сравниваемый уровень больше или меньше предыдущего (базисного). Между базисными и цепными темпами роста имеется взаимосвязь: произведение последовательных цепных темпов роста равно последнему базисному темпу роста.
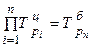 .
.
Темпы прироста характеризуют абсолютный прирост в относительных величинах. Темп прироста равен отношению абсолютного прироста к уровню ряда, принятому за базу сравнения.
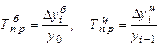 .
.
Темп прироста показывает на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения.
Между темпами роста и прироста имеется взаимосвязь.
 .
.
Значение цепных темпов прироста, рассчитанных каждый к своей базе, различаются не только числом процентов, но и величиной абсолютного изменения, составляющего каждый процент.
Абсолютное значение одного процента прироста 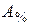 выражается отношением абсолютного прироста к темпу прироста. Расчет этого показателя имеет экономический смысл только на цепной основе.
выражается отношением абсолютного прироста к темпу прироста. Расчет этого показателя имеет экономический смысл только на цепной основе.
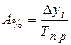 .
.
Для получения обобщающих показателей динамики социально-экономических явлений применяются средние величины: средний уровень, средний абсолютный прирост, средний темп роста и прироста и другие.
Средний уровень ряда (средняя хронологическая) рассчитывается в зависимости от вида ряда динамики. В интервальном ряду динамики расчет среднего уровня ряда производится по методу средней арифметической простой.
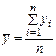 , где
, где 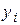 - уровни ряда; n - число уровней.
- уровни ряда; n - число уровней.
В моментном ряду динамики с равноотстоящими датами средний уровень ряда определяется по формуле средней хронологической.
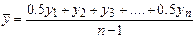 .
.
В практике экономической работы часто приходится определять средние уровни ряда моментных величин с неравноотстоящими датами времени. Расчет среднего уровня в таких рядах динамики производится по методу средней арифметической взвешенной.
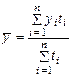 ,
,
где 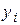 - уровни ряда динамики, сохраняющиеся без изменения в течение промежутков (интервалов) времени
- уровни ряда динамики, сохраняющиеся без изменения в течение промежутков (интервалов) времени 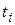 .
.
Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики.
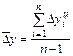 ,
, 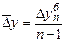 .
.
Средний темп роста - обобщающая характеристика индивидуальных темпов роста ряда динамики.
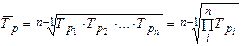 ,
,
где n - число уровней ряда; 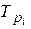 - цепные темпы роста.
- цепные темпы роста.
На основе взаимосвязи между цепными и базисными темпами роста средний темп роста можно определить по формуле:
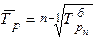 .
.
Средний темп прироста можно определить на основе взаимосвязи между темпами роста и прироста.
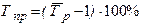 .
.
Абсолютным ускорением называется разность между двумя абсолютными приростами.
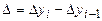 .
.
Относительным ускорением называется отношение абсолютного ускорения к абсолютному приросту, принятому за базу.
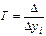 .
.
Пример 1. Ряд динамики розничного товарооборота магазина характеризуется следующими данными:
| Период | I | II | III | IV | V |
| Объем товарооборота, тыс. руб. | 885.7 | 932.6 | 980.1 | 1028.7 | 1088.4 |
Необходимо рассчитать абсолютные и относительные показатели ряда динамики. Представим расчеты в виде таблицы.
| Период | Товарооборот, тыс.руб. | Абсолютный прирост, тыс. руб. | Темп роста, % | Темп прироста, % | Темп наращивания | |||
| Б | Ц | Б | Ц | Б | Ц | |||
| I | 885.7 | - | - | - | - | - | - | - |
| II | 932.6 | 46.9 | 46.9 | 105.3 | 105.3 | 5.3 | 5.3 | 5.3 |
| III | 980.1 | 94.4 | 47.5 | 110.6 | 105.1 | 10.6 | 5.1 | 5.4 |
| IV | 1028.7 | 143.0 | 48.6 | 116.1 | 104.9 | 16.1 | 4.9 | 5.5 |
| V | 1088.4 | 202.7 | 59.7 | 122.9 | 105.8 | 22.9 | 5.8 | 6.8 |
Из таблицы видно, что по сравнению с первым периодом в каждом последующем периоде происходило систематическое увеличение абсолютных приростов товарооборота (тыс.руб.): 46.9<94.4<143.0<202.7.
Цепные абсолютные приросты показывают, что нарастание объемов товарооборота происходило из периода в период: 46.9<47.5<48.6<59.7.
Абсолютный прирост может иметь и отрицательный знак, показывающий на сколько уровень текущего периода ниже базисного. По цепным абсолютным приростам определяется базисный абсолютный прирост:
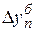 = 46.9+47.5+48.6+59.7 = 202.7 тыс. руб.
= 46.9+47.5+48.6+59.7 = 202.7 тыс. руб.
В V периоде по сравнению с I периодом товарооборот увеличился на 202.7 тыс.руб. Базисные темпы роста показывают, что по сравнению с I периодом происходило систематическое увеличение товарооборота магазина, достигшего в V периоде 122.9% базисного уровня. Цепные темпы роста показывают, что в развитии товарооборота имело место замедление темпов (%): 105.3>105.1>104.9<105.8. Проверим связь цепных и базисных темпов роста: 1.053×1.051×1.049×1058 = 1.229.
Средний уровень ряда: 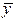 =(885.7+...+1088.4):5=983.1 тыс.руб. С I периода по V период товарооборот в среднем составлял 983.1 тыс. руб. Средний абсолютный прирост:
=(885.7+...+1088.4):5=983.1 тыс.руб. С I периода по V период товарооборот в среднем составлял 983.1 тыс. руб. Средний абсолютный прирост: 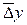 =(46.9+47.5+48.6+59.7):4=50.7 тыс. руб. (
=(46.9+47.5+48.6+59.7):4=50.7 тыс. руб. (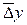 =(1088.4-885.7):4=50.7 тыс. руб.). С I периода по V период ежегодно объем товарооборота возрастал в среднем на 50.7 тыс. руб. Средний темп роста:
=(1088.4-885.7):4=50.7 тыс. руб.). С I периода по V период ежегодно объем товарооборота возрастал в среднем на 50.7 тыс. руб. Средний темп роста: 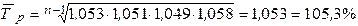 . С I периода по V период товарооборот ежегодно возрастал в среднем в 1.053 раза или на 5.3 %.
. С I периода по V период товарооборот ежегодно возрастал в среднем в 1.053 раза или на 5.3 %.
Важной задачей статистики при анализе рядов динамики является определение общей тенденции развития. На развитие явления во времени могут оказывать влияние различные по своему характеру и силе воздействия факторы. Одни из них оказывают более или менее постоянное воздействие и формируют в рядах динамики определенную тенденцию развития (тренд). Воздействие же других факторов может быть кратковременным.
При изучении колеблемости цен в динамике определяется тенденция их изменения во времени. Тренд, вокруг которого варьируют цены, рассматривается как общая закономерность динамики цен. Основные способы статистического выявления тренда заключается в укрупнении интервалов, сглаживании ряда с помощью скользящей средней и аналитическом выравнивании.
В общем виде трендовая модель для отдельной цены или индекса цен может быть выражена как функция 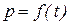 , где t - номер периода. Модель отражает не только направление изменения, но и его характер (ускорение, замедление), а также дает количественную оценку среднего изменения за период, которая определяется как первая производная соответствующей функции.
, где t - номер периода. Модель отражает не только направление изменения, но и его характер (ускорение, замедление), а также дает количественную оценку среднего изменения за период, которая определяется как первая производная соответствующей функции.
Метод укрупнения интервалов применяется для выявления тренда в рядах динамики колеблющихся уровней, затушевывающих основную тенденцию развития. Этот метод основан на укрупнении периодов, к которым относятся уровни ряда динамики.
Пример 2. Имеются данные о реализации товаров в одном из магазинов города.
| Январь | 23.2 | июль | 28.4 |
| февраль | 19.1 | август | 24.1 |
| Март | 22.3 | сентябрь | 26.3 |
| Апрель | 25.1 | октябрь | 29.1 |
| Май | 24.5 | ноябрь | 30.3 |
| Июнь | 27.3 | декабрь | 26.5 |
Различные направления изменений по отдельным месяцам уровней данного ряда динамики затрудняют выводы об основной тенденции продажи товаров. Для выявления общей тенденции реализации товаров произведем укрупнение интервалов. Для этой цели исходные (месячные) данные о реализации товаров преобразуем в квартальные.
| 1 кв. | 2 кв. | 3 кв. | 4 кв. |
| 64.5 | 76.9 | 78.8 | 85.9 |
В результате укрупнения интервалов общая тенденция роста продажи товаров становится очевидной. 64.5 < 76.9 < 78.8 < 85.9.
Для статистического изучения тренда применяется так называемое сглаживание методом скользящей средней. Сущность метода состоит в том, что по исходным уровням ряда (эмпирическим данным) определяют расчетные (теоретические) уровни, в которых случайные тенденции погашаются, а основная тенденция развития выражается в виде некоторой плавной линии.
Применение этого метода рассмотрим на данных о реализации продуктов.
| Квартал | 1 год | 2 год | 3 год | 4 год |
Для выражения общей тенденции развития явления методом сглаживания рядов динамики необходимо, прежде всего определить по исходным данным подвижные (скользящие) средние. Основное условие применения этого метода состоит в вычислении звеньев скользящей средней.
Для ряда внутригодовой динамики с сезонными циклами развития явления по кварталам применяют четырехчленные скользящие средние. Их расчет состоит в определении средних величин из 4-х уровней ряда с отбрасыванием при вычислении каждой новой скользящей средней одного уровня слева и присоединением одного уровня справа:
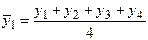 ;
; 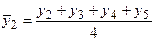 .
.
Расчет скользящих средних представим в таблице.
| Период | Исходные уровни у | Скользящие средние у0 | Сглаженные уровни уi |
| 1 год 1 кв. | |||
| 2 кв. | 1061:4=265.25 | ||
| 3 кв. | 1133:4=283.25 | (265.25+283.25):2=274.25 | |
| 4 кв. | 1168:4=292.00 | (283.25+292.00):2=287.6 | |
| 2 год 1 кв. | 1208:4=302.00 | 297.0 | |
| 2 кв. | 1252:4=313.00 | 307.5 | |
| 3 кв. | 1425:4=356.25 | 334.6 | |
| 4 кв. | 1568:4=392.00 | 374.1 | |
| 3 год 1 кв. | 1655:4=413.75 | 402.9 | |
| 2 кв. | 1713:4=428.25 | 421.0 | |
| 3 кв. | 1719:4=429.25 | 429.0 | |
| 4 кв. | 430.75 | ||
| 4 год 1 кв. | 1727:4=431.75 | 435.37 | |
| 2 кв. | 1756:4=439.00 | 446.62 | |
| 3 кв. | 1817:4=454.25 | ||
| 4 кв. |
Для определения сглаженных уровней производится центрирование. Если при сглаживании рядов динамики звенья скользящей средней составляются из нечетного числа уровней, то необходимость в центрировании отпадает. Применение в анализе рядов динамики методов укрупнения интервалов и скользящей средней позволяет выявить тренд для его описания, но получить обобщенную статистическую оценку тренда с помощью этих методов невозможно.
Изменение тренда достигается с помощью метода аналитического выравнивания. Основным содержанием метода аналитического выравнивания в рядах динамики является то, что основная тенденция развития 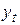 рассчитывается как функция времени
рассчитывается как функция времени 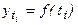 . Определение теоретических уровней
. Определение теоретических уровней 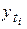 производится на основе так называемой адекватной математической функции, которая наилучшим образом отображает основную тенденцию развития ряда динамики. Допустим, что функция имеет вид прямолинейного тренда:
производится на основе так называемой адекватной математической функции, которая наилучшим образом отображает основную тенденцию развития ряда динамики. Допустим, что функция имеет вид прямолинейного тренда: 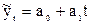 . Для нахождения
. Для нахождения 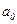 и
и 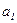 составляем систему уравнений
составляем систему уравнений
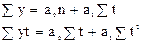
Если тенденция явления имеет вид параболы 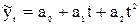 , то для нахождения
, то для нахождения 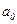 ,
, 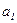 и
и 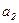 составляем систему уравнений
составляем систему уравнений
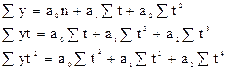
Пример 3. Имеются данные о выпуске продукции предприятиями легкой промышленности за ряд периодов в сопоставимых ценах, млн. руб.
| I | II | III | IV | V | VI | VII | VIII | IX |
Иногда для простоты расчетов можно решить систему уравнений, приняв 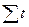 =0. Для расчета составим рабочую таблицу:
=0. Для расчета составим рабочую таблицу:
| Период | Эмпирические значения | Условные обозначения времени t | t | yt | yt |
| I | -4 | -884 | 219.32 | ||
| II | -3 | -705 | 241.24 | ||
| III | -2 | -544 | 263.16 | ||
| IV | -1 | -285 | 285.08 | ||
| V | 307.0 | ||||
| VI | 328.92 | ||||
| VII | 350.84 | ||||
| VIII | 372.76 | ||||
| IX | 394.68 | ||||
| Итого |
Вычислим значения: 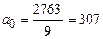 ;
; 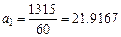 . Подставив
. Подставив 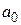 ,
, 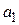 в исходное линейное уравнение, получим:
в исходное линейное уравнение, получим: 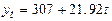 .
.
Важное место в анализе рядов динамики занимает изучение сезонных колебаний с помощью индексов сезонности. По данным одного года индексы сезонности рассчитываются как процентное отношение помесячных уровней к среднему уровню за год, т.е. 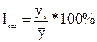 . Для большей надежности сезонность изучается по данным за три года. В этом случае для каждого месяца рассчитывается средний уровень за три года, который и сопоставляется со средним уровнем за весь период
. Для большей надежности сезонность изучается по данным за три года. В этом случае для каждого месяца рассчитывается средний уровень за три года, который и сопоставляется со средним уровнем за весь период 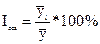 .
.
Чтобы учесть и имеющую место тенденцию изменения, рекомендуется производить сглаживание ряда способом скользящей средней или по аналитическим формулам, а затем находить отношение фактического уровня каждого месяца к выровненному, т.е.
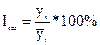 .
.
Для учета сезонной волны при прогнозировании из полученных отношений для одноименных месяцев (кварталов) рассчитывается средняя величина.
| Квартал | 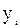 | 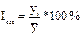 | Средние индексы сезонности  |
| 2001-1 2002-1 | 298.8 228.9 118.4 270.4 307.3 301.5 152.7 286.2 | 121.7 93.2 48.2 110.1 125.2 122.8 62.2 116.5 | 123.45 108.00 55.20 113.30 123.45 108.00 55.20 113.30 |
| Всего | 1964.2 | - |
1. Рассчитываем средний квартальный уровень за два года. 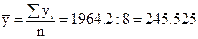 .
.
2. Рассчитываем индексы сезонности (гр.3).
3. По данным двух лет рассчитываем средний индекс для каждого квартала.
Поскольку в квартальных уровнях имеется тенденция к снижению, то рекомендуется произвести аналитическое выравнивание ряда, а затем индексы сезонности рассчитать как отношение к выровненным уровням, а не к общей средней. Для выравнивания примем линейную функцию. Если тренд в виде прямой, то 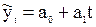 . Для нахождения
. Для нахождения 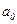 и
и 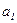 составляем систему уравнений, а затем рабочую таблицу.
составляем систему уравнений, а затем рабочую таблицу.
| Квартал | 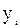 | 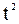 | 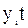 | 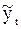 | 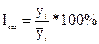 | Средние индексы сезонности 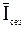 | Выровненные уровни 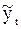 с учетом сезонности с учетом сезонности |
| 8=гр.5*гр.7 | |||||||
| 298.8 228.9 118.4 270.4 307.3 301.5 152.7 286.2 | 298.8 457.8 355.2 1081.6 1536.5 1809.0 1068.9 2289.6 | 240.62 242.02 243.42 244.82 246.22 247.62 249.02 250.42 | 124.2 94.6 48.6 110.4 124.8 121.8 61.3 114.3 | 124.5 108.2 55.0 112.4 124.5 108.2 55.0 112.4 | 299.6 261.9 133.9 275.2 306.5 267.9 137.0 281.5 | ||
| 1964.2 | 8897.4 | 1964.2 | - | - | 1963.5 |
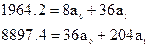 Уравнение тренда примет вид
Уравнение тренда примет вид 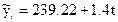
Лекция 8, 9. Одной из важнейших задач статистики является изучение развития процессов и явлений во времени. Это осуществляется с помощью построения и анализа статистических рядов динамики. На развитие явления во времени могут оказывать влияние различные по своему характеру и силе воздействия факторы. Одни из них оказывают более или менее постоянное воздействие и формируют в рядах динамики определенную тенденцию развития (тренд). Воздействие же других факторов может быть кратковременным. Основные способы статистического выявления тренда заключается в укрупнении интервалов, сглаживании ряда с помощью скользящей средней и аналитическом выравнивании. Важной проблемой является подбор математической функции, по которой рассчитываются теоретические уровни тренда. От правильности решения этой проблемы зависят выводы о закономерностях тренда изучаемых явлений.
При изучении данной темы необходимо обратить особое внимание на расчет показателей динамики, их дифференциацию на абсолютные и относительные, цепные и базисные.; на выявление основной тенденции и экстраполяции на основе рядов динамики.
Практическое занятие 6. Решение задач по теме.
Задание 1. Имеются данные о производстве кожаной обуви в республике Беларусь:
| Объем производства, млн пар | 45,3 | 37,2 | 33,4 | 26,4 | 16,5 | 13,0 | 11,4 | 11,2 | 13,2 |
| Периоды |
Определить:
- аналитические показатели абсолютного прироста, темпа роста, темпа прироста;
- средний абсолютный прирост, средний темп роста, средний темп прироста;
- составить уравнение тренда, определить прогноз на 2009 год.
Задание 2. Существуют данные о грузообороте транспорта в Российской Федерации (тыс. т).
| Месяцы | |||
| Январь | 277.8 | 276.7 | |
| Февраль | 266.8 | 250.5 | 250.9 |
| Март | 288.5 | 282.3 | 289.6 |
| Апрель | 264.8 | 275.5 | |
| Май | 267.4 | 257.5 | 280.6 |
| Июнь | 255.8 | 254.5 | 268.8 |
| Июль | 260.1 | 256.9 | 273.1 |
| Август | 256.9 | 256.9 | 278.2 |
| Сентябрь | 261.2 | 245.9 | 271.7 |
| Октябрь | 274.4 | 274.2 | 289.6 |
| Ноябрь | 279.1 | 269.6 | 286.1 |
| Декабрь | 289.4 | 279.5 | 303.8 |
Для изучения общей тенденции грузооборота транспорта в РФ:
1. Рассчитать показатели динамики по годам и сделать вывод.
2. Провести преобразование исходных данных путем укрупнения периодов времени в квартальные уровни. Нанести на график полученные квартальные уровни.
3. Произвести сглаживание квартальных уровней методом скользящей средней. Нанести полученные при сглаживании данные на график с квартальными уровнями.
4. Составить уравнение линейного тренда. Составить прогноз на 2006 год.
Задание 3. Ежедневное поступление за март в областной бюджет по всем видам налогов (тыс. руб.) представлено в таблице.
| 01.03 | 02.03 | 05.03 | 06.03 | 07.03 | 11.03 | 12.03 | 13.03 | 14.03 | 15.03 | 16.03 |
| 19.03 | 20.03 | 21.03 | 22.03 | 23.03 | 26.03 | 27.03 | 28.03 | 29.03 | 30.03 |
На основании приведенных данных проведите исследование ряда динамики.
Задание 4. В виде таблицы приведены данные о потреблении продуктов питания на территории РФ (в среднем на душу населения).
| Продукты питания | |||||||
| Хлеб | |||||||
| Картофель | |||||||
| Овощи | |||||||
| Молоко | |||||||
| Яйца (шт.) | |||||||
| Сахар | |||||||
| Мясо |
Выполнить анализ ряда динамики.
Задание 5. Ниже приведены данные о доходах парка аттракционов в городе (тыс. руб.).
| Месяцы | Аттракционы | ||
| Январь | 5.2 | 8.3 | |
| Февраль | 17.5 | ||
| Март | 11.5 | 14.4 | 14.7 |
| Апрель | 88.9 | ||
| Май | 100.5 | ||
| Июнь | 400.9 | ||
| Июль | |||
| Август | 570.4 | ||
| Сентябрь | 200.5 | ||
| Октябрь | 105.7 | 99.7 | |
| Ноябрь | 15.9 | 20.4 | |
| Декабрь | 9.3 |
Произведите анализ сезонных колебаний и постройте график сезонной волны по каждому году.
Задание 6. Численность населения двух городов составляла (тыс. чел.):
| город А | город В | |
| на 1 января 2006 г. | 75.0 | 151.1 |
| на 1 апреля | 75.1 | 151.3 |
| на 1 июля | 75.2 | 151.2 |
| на 1 октября | 75.5 | 152.0 |
| на 1 января 2007 г. | 75.8 | 152.1 |
Определить среднюю численность населения за каждое полугодие 2006 года и за год в целом. Рассчитать темпы роста численности населения городов. Выполнить анализ.
Лабораторная работа 3. Комплексный анализ ряда динамики, прогноз развития конкретного социально – экономического явления.
Самостоятельная работа: написание эссе, составление алгоритма.
Подробное изложение материала по теме представлено в основной литературе обязательная - [2,7,10], 7 – стр.142 – 168, - дополнительная - [8, 9].
Для закрепления теории необходимо ответить на основные вопросы:
1. В чем состоит значение рядов динамики (РД). Какие принципы составления РД вы знаете.
2. Как дифференцируются ряды динамики.
3. Какие показатели применяются для характеристики ряда динамики.
4. Какие виды средних используются для расчета среднего уровня рядов динамики.
3. Что такое цепная и базисная основа расчета показателей динамики?
4. Перечислите аналитические показатели РД.
5. Какие свойства показателей РД вы знаете.
6. Какие вы знаете методы выявления и анализа основной тенденции ряда динамики.
7. Какова роль аналитического выравнивания уровней ряда динамики.
8. Как выполнить прогноз на будущее с помощью уравнения тренда.
9. Какие методы могут быть использованы для выявления сезонных колебаний.
 2015-03-08
2015-03-08 3279
3279
