Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, т. е. их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).
Ряд динамики (временной ряд) представляет собой ряд, рacположенных в хронологической последовательности числовых значений статистического показателя, характеризующего изменение изучаемого явления во времени.
Ряд динамики может быть изображен графически, что позволяет, наглядно представить развитие явления во времени. Чаще используются линейные диаграммы: по оси абсцисс отмечается время, по оси ординат - уровни ряда. Широко используются также столбиковые, секторные и другие диаграммы.
В каждом ряду динамики имеются два основных элемента:
1) показатель времени t;
2) уровень ряда у.
Показателями времени могут быть периоды (год, квартал, месяц, сутки) и моменты (определенная дата на начало или конец периода).
Уровень ряда - это размер (объем, величина) того или иного явления (показателя), достигнутый за определенный период времени или к определенному моменту. Уровни в динамическом ряду могут быть представлены абсолютными, относительными или средними величинами.
По времени ряды разделяются на моментные и интервальные.
Моментным называется ряд динамики, уровни которого характеризуют состояние явления на определенные даты(моменты времени). Например, число нерассмотренных дел в суде, находящихся в остатке на конец отчетного периода – на 1 июля 2010 г., число приостановленных дел на данную дату, число лиц, находящихся в розыске на отчетную дату).
Интервальным (периодическим) рядом динамики называется такой ряд, уровни которого характеризуют размер явления за конкретный период времени (год, квартал, месяц). Например, число рассмотренных гражданских дел с вынесением решения за 2009 год мировыми судьями или число лиц, в отношении которых были вынесены оправдательные приговоры по первой инстанции в 1 полугодии 2010 г.
Для количественной оценки динамики правовых явлений применяются такие статистические показатели как абсолютные приросты, темпы роста, темпы прироста, которые делятся на базисные, цепные и средние. В основе расчета этих показателей динамики лежит сравнение уровней ряда динамики. Если сравнение осуществляется с одним и тем же уровнем, принятым за базу сравнения, то эти показатели называются базисными. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень с которого начинается какой-то новый этап развития явления (например, число осужденных по статьям УК РФ с 1997 года – года вступления в силу нового Уголовного кодекса). Если сравнение осуществляется при переменной базе и каждый последующий уровень ряда сравнивается с предыдущим, то вычисленные таким образом показатели динамики называются цепными.
Для рядов динамики со значительными колебаниями уровней в качестве базы сравнения применяются средние уровни.
Абсолютный прирост (Δу) равен разности двух сравниваемых уровней.
Базисный абсолютный прирост
Δyiб = yi - yб.
Цепной абсолютный прирост
Δyi = yi - yi - 1.
где yi - уровень сравниваемого периода;
yi-1 - уровень предшествующего периода;
yб - уровень базисного периода;
n - число уровней ряда.
Темп роста - это отношение уровня ряда одного периода к уровню ряда другого периода, выраженное в процентах.
Базисный темп роста Tiб=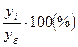
Цепной темп роста Ti=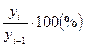
Средний темп роста 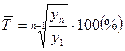
Замечание. Если темп роста и средний темп роста вычисляются в долях (не умножаются на 100%), то они называются соответственно коэффициентом роста и средним коэффициентом роста.
Темп прироста вычисляется как отношение абсолютного прироста (Δу) к уровню, принятому за базу сравнения. Темп прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения. Он может быть положительным, отрицательным или равным нулю.
Базисный темп прироста Тпр iб=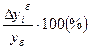
Цепной темп прироста Тпр i=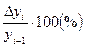
Средний темп прироста 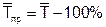 .
.
Замечание. Если вычислен соответствующий темп роста, то темп прироста равен:
Тпр.= Тр. - 100%.
Пример. Рассчитать абсолютные приросты, темпы роста и темпы прироста числа осужденных за взяточничество базисным и цепным способом, используя данные таблицы 8. За базу взять 2004 год.
Используя приведенные выше формулы, получим:
Базисный абсолютный прирост
Δyб2002 = y2002 - y2004 = 2035 - 2930 = - 895, Δyб2003 = y2003 - y2004 = 2232 - 2930 = - 698,
Δyб2005 = y2005 - y2004 = 3609 - 2930 = 679, Δyб2006 = y2006 - y2004 = 4229 - 2930 = 1299.
Цепной абсолютный прирост
Δy2003 = y2003 - y2002 = 2232 - 2035 = 197, Δy2004 = y2004 - y2003 = 2930 - 2232 = 698,
Δy2005 = y2005 - y2004 = 3609 - 2930 = 679 , Δy2006 = y2006 - y2005 = 4229 - 3609 = 620.
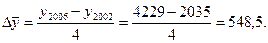
Базисный темп роста
Tб2002=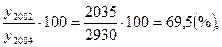 Tб2003=
Tб2003=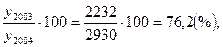 Tб2005=
Tб2005=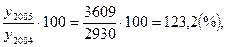 Tб2006=
Tб2006=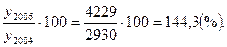
Цепной темп роста
T2003=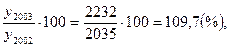 T2004=
T2004=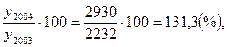
T2005=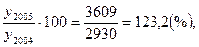 T2006=
T2006=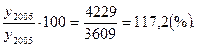
Средний темп роста 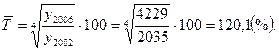
Базисный темп прироста
Тпрб2002=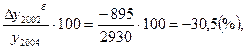 Тпрб2003=
Тпрб2003=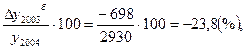
Тпр б2005=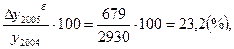 Тпрб2006=
Тпрб2006=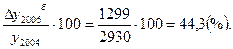
Цепной темп прироста
Тпр2003=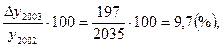 Тпр 2004=
Тпр 2004=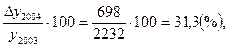
Тпр 2005=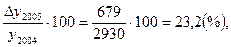 Тпр2006=
Тпр2006=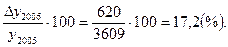
Средний темп прироста 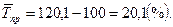
Наряду с указанными показателями в ряду динамики может быть рассчитан средний уровень ряда. Он применим для любого ряда динамики: интервального и моментного.
В интервальных рядах динамики средний уровень (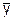 ) определяется делением суммы уровней ряда на их число, т. е. по методу средней арифметической:
) определяется делением суммы уровней ряда на их число, т. е. по методу средней арифметической:
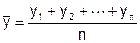
yi - абсолютные уровни ряда; n - число уровней.
В моментном ряду с равными интервалами времени средний уровень - средняя хронологическая моментного ряда - определяется по формуле:
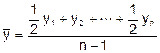
В моментном ряду с неравными интервалами времени средний уровень ряда определяется по формуле средней арифметической взвешенной
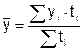
где yi - уровни ряда динамики, сохранившиеся без изменения в течение промежутка времени ti.
Пример. Рассчитатьсредний уровень ряда числа осужденных за взяточничество, используя данные таблицы 8.
Используя приведенную выше формулу для интервального ряда динамики, получим:
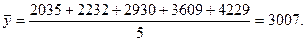
На практике принято считать, что значения уровней рядов динамики статистических показателей формируются под воздействием следующих компонент: тренда, сезонной, циклической и случайной составляющих. В большинстве случаев фактический уровень ряда динамики можно представить как сумму или произведение указанных выше компонентов. Модель, в которой ряд динамики представлен как сумма перечисленных компонент, называется аддитивной моделью ряда динамики. Модель, в которой ряд динамики представлен как произведение перечисленных компонент, называется мультипликативной моделью ряда динамики. Основная задача исследования отдельного ряда динамики – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда.
Под трендом понимают плавноеизменение, определяющее общее направлениеразвития, основную тенденцию ряда динамики. Это систематическая составляющая, характеризующая долговременное воздействие факторов на динамику изучаемого показателя.
Наряду с долговременными тенденциями во временных рядах социальных процессов часто имеют место более или менее регулярные колебания - периодические составляющие рядов динамики.
Если период колебаний не превышает одного года, то их называют сезонными. Чаще всего причиной их возникновения считаются природно-климатические условия, обуславливающие социально-экономические явления (в сезон отпусков увеличивается количество квартирных краж, уменьшается число подаваемых в суды исков от физических лиц и т.п.).
При большем периоде колебания, считают, что в рядах динамики имеет место циклическая составляющая. Примерами могут служить демографические, инвестиционные и другие циклы.
Если из временного ряда удалить тренд и периодические составляющие, то останется случайная компонента, являющаяся результатом действия большого числа побочных факторов. Влияние каждого из таких факторов незначительно, но ощущается их суммарное воздействие. В судебной статистике одним из таких случайных факторов, который может оказывать существенное влияние на динамику, является изменение законодательства.
Важной задачей, решаемой с использованием рядов динамики, является определение общей тенденции развития, т.е. тренда. Выявление тренда в статистике называют также выравниванием ряда динамики, а методы выявления основной тенденции – методами выравнивания.
Выравнивание можно осуществлять разными способами: методом укрупнения интервалов, сглаживанием методом скользящей средней или аналитическим выравниванием.
Метод укрупнения интервалов заключается в преобразовании первоначального ряда динамики в ряд более продолжительных периодов (месячные в квартальные, квартальные в годовые и т. д.).
Метод скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по счету уровней, затем из такого же числа уровней, но начиная со второго по счету далее - начиная с третьего и т. д. Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один уровень. Например,
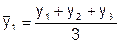 ,
, 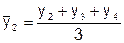 ,
, 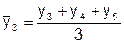 , и.т.д.
, и.т.д.
Первые два метода дают возможность определить лишь общую тенденцию развития явления, но получить обобщенную статистическую модель тренда посредством этих методов нельзя. Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени используется аналитическое выравнивание ряда динамики.
Основным содержанием метода является то, что математическая модель тренда представляется в виде некоторой функции времени 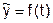 , которая наилучшим образом отображает (аппроксимирует) основную тенденцию развития ряда динамики. Выбор типа модели должен быть основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики (линейной диаграмме). Подбор адекватной функции осуществляется методом наименьших квадратов - минимальностью суммы квадратов отклонений между расчетными
, которая наилучшим образом отображает (аппроксимирует) основную тенденцию развития ряда динамики. Выбор типа модели должен быть основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики (линейной диаграмме). Подбор адекватной функции осуществляется методом наименьших квадратов - минимальностью суммы квадратов отклонений между расчетными 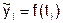 и фактическими yi уровнями ряда динамики:
и фактическими yi уровнями ряда динамики:
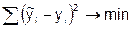
Основными моделями общей тенденции рядов динамики являются следующие:
1. Равномерное развитие отображается уравнением прямолинейной функции 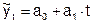 ,
,
где ао и а1 - параметры уравнения, t - время.
Параметр а1 определяет направление развития. Если а1 > О, то уровни ряда динамики равномерно возрастают, если а1 < О - происходит их равномерное снижение.
Модель равномерного развития общей тенденции применяется для рядов динамики с постоянными абсолютными приростами.
2. Равноускоренное (равнозамедленное) развитие отображается уравнением параболы второго порядка
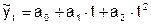
Параметр а2 характеризует постоянное изменения интенсивности развития (в единицу времени). Уровни рядов динамики, для которых используется такая модель общей тенденции развития, изменяются с постоянными темпами прироста.
3. Развитие по экспоненте отображается показательной функцией
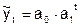
где а1 - темп роста (снижения) изучаемого явления в единицу времени, т. е. интенсивность развития. Для этой модели общей тенденции развития уровням ряда динамики присущи постоянные темпы роста.
Применяются и другие математические функции.
Выявленные при анализе рядов динамики закономерности могут служить базой для прогнозирования развития изучаемого явления в будущем. Основой прогнозирования является предположение, что закономерность, действующая внутри анализируемого ряда динамики, выступающего в качестве базы прогнозирования, сохраняется в дальнейшем.
Грубый прогноз можно получить на основе средних показателей ряда.
При прогнозировании на базе ряда динамики с постоянным абсолютным приростом применяется формула:
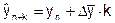 ,
,
где 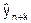 - прогнозируемый уровень ряда,
- прогнозируемый уровень ряда,
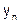 - фактическое значение последнего уровня ряда динамики,
- фактическое значение последнего уровня ряда динамики,
k - срок прогноза (период упреждения).
При прогнозировании на базе ряда динамики с постоянными темпами роста применяется следующая формула:
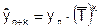 ,
,
где 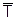 - средний коэффициент роста (цепной) ряда динамики, выступающего в качестве базы прогнозирования.
- средний коэффициент роста (цепной) ряда динамики, выступающего в качестве базы прогнозирования.
Для более точного прогнозаиспользуются, например, такие статистические методы прогнозирования как метод кривых роста и адаптивные методы.
Пример. Принимая во внимание, что цепные темпы роста числа осужденных за взяточничество приблизительно одинаковы, построим грубый прогноз на 2007 год.
Используя соответствующую формулу, получим:

Таким образом, число осужденных за взяточничество (ст. 290, 291 УК РФ) в 2007 году приблизительно должно было составить 5075 человек. (По данным статистического сборника «Преступность и правонарушения (2004-2008)» число осужденных по приговорам вступившим в законную силу в 2007 г. по основной квалификации составило 4869.)
1. Федеральный закон «Об официальном статистическом учете и системе государственной статистики» от 29.11.2007 № 282-ФЗ.
2. Указ Президента Российской Федерации от 30.марта1998 № 328 «О разработке единой государственной системы регистрации и учета преступлений».
3. Постановление Правительства РФ от 02.06.2008 г. № 420 «О Федеральной службе государственной статистики»
4. Инструкция по судебному делопроизводству в районном суде, утвержденная приказом Судебного департамента при Верховном Суде Российской Федерации от 29.04.03 № 36
5. Инструкция по судебному делопроизводству в верховных судах республик, краевых и областных судах, судах городов федерального значения, судах автономной области и автономных округов», утвержденная приказом Судебного департамента при Верховном Суде Российской Федерации от 12.12.2004 № 161
6. Приказ Судебного департамента при Верховном Суде Российской Федерации от 16.10.2009 № 187 «Об утверждении статистической карточки на подсудимого»
7. Инструкция по ведению судебной статистики, утвержденная приказом Судебного департамента при Верховном Суде Российской Федерации от 29.12.2007 г. № 169
8. Постановление Федеральной службы государственной статистики от 15.01.2008 г. № 4 «Об утверждении статистического инструментария для организации статистического наблюдения за регистрацией уголовных дел и учетом преступлений»
9..Приказ Судебного департамента при Верховном Суде Российской Федерации от 20.05.2009 № 97 «Об утверждении Табеля форм статистической отчетности о деятельности федеральных судов общей юрисдикции и мировых судей, образцов форм статистической отчетности», с изменениями, внесенными приказом Судебного департамента № 130 от 23 июня 2010 г. (Приказы и образцы форм статистической отчетности размещены на Интернет-сайте Судебного департамента www.cdep.ru раздел «Судебная статистика»).
Основная
1. Ловцов Д.А., Богданова М.В. Юридическая статистика: Тексты лекций.– М.: РАП, 2007.
2. Лунеев В.В. Юридическая статистика -М.: Юристъ, 2007.
3. Савюк Л.К. Правовая статистика. -М.: Юристъ, 2007
 2014-02-02
2014-02-02 22807
22807
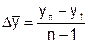
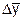 -
-