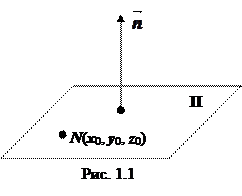
 1.1.1. Если плоскость П проходит через точку N (x 0, y 0, z 0) перпендикулярно вектору
1.1.1. Если плоскость П проходит через точку N (x 0, y 0, z 0) перпендикулярно вектору 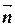 =(A, B, C) (рис. 1.1), то общее уравнение плоскости П имеет вид
=(A, B, C) (рис. 1.1), то общее уравнение плоскости П имеет вид
A (x - x 0)+ B (y - y 0)+ С (z - z 0)=0. (1.1)
Как правило, общее уравнение (1.1) прямой приводят к виду
Ax + By + Сz + D =0, (1.2)
где D =- Ax 0- By 0- Сz 0.
Вектор 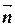 =(A, B, C) называется вектором нормали (или нормалью) плоскости П.
=(A, B, C) называется вектором нормали (или нормалью) плоскости П.
1.1.2. Если плоскость П проходит через точку N (x 0, y 0, z 0) параллельно неколлинеарным векторам 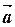 =(ax, ay, az),
=(ax, ay, az), 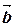 =(bx, by, bz) (рис.1.2), то параметрические уравнения плоскости П имеют вид
=(bx, by, bz) (рис.1.2), то параметрические уравнения плоскости П имеют вид
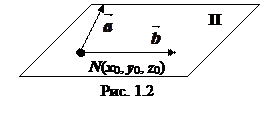
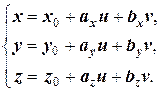 (1.3)
(1.3)
Векторы 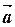 =(ax, ay, az) и
=(ax, ay, az) и 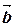 =(bx, by, bz) называются направляющимивекторами плоскости П.
=(bx, by, bz) называются направляющимивекторами плоскости П.
1.1.3. Уравнение плоскости можно записать и в явном виде z = ax + by + c, но в отличие от случая прямой оно не представляет особый интерес.
1.1.4. Кроме приведённых выше видов уравнений плоскости также рассматриваются другие виды:
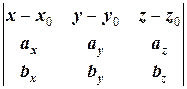 =0, (1.4)
=0, (1.4)
где (x 0, y 0, z 0), 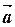 =(ax, ay, az),
=(ax, ay, az), 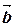 =(bx, by, bz) - как в уравнениях (1.3);
=(bx, by, bz) - как в уравнениях (1.3);
уравнение плоскости, проходящей через три точкиN (x 0, y 0, z 0), M (x 1, y 1, z 1), L (x 2, y 2, z 2):
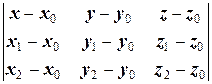 =0, (1.5)
=0, (1.5)
где точки N, M, L не лежат на одной прямой;
уравнение плоскости в отрезках: 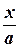 +
+ 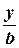 +
+ 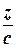 =1, (1.6)
=1, (1.6)
при условии, что плоскость не параллельна ни одной из осей координат.
1.1.5. Замечания. 1) Как и в случае уравнений прямой, с помощью тождественных преобразований из одного вида уравнений можно прийти к другому.
2) В частных случаях, когда плоскость параллельна одной из координатных плоскостей, общее уравнение (1.2) записывается в виде x = a (если плоскость параллельна плоскости Oyz), y = b (если плоскость параллельна плоскости Oxz) или z = c (если плоскость параллельна плоскости Oyz).
3) Уравнения (1.4) и (1.5), как правило, приводятся к общему виду. Для этого достаточно расписать определители в левых частях этих уравнений и привести подобные относительно x, y, z и свободных членов.
4) Геометрический смысл параметров a, b и с в уравнении (1.6) следующий: a, b и с - соответственно абсцисса, ордината и аппликата точек пересечения плоскости с осями соответственно Ox, Oy и Oz.
1.1.6. Упражнения. 1) Написать общее уравнение плоскости:
а) проходящей через точку N (3; -2; 4) перпендикулярно вектору 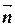 =(4; -2, 8);
=(4; -2, 8);
б) проходящей через точку N (2; 4; -3) перпендикулярно вектору 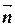 =(3; 8; -4).
=(3; 8; -4).
Решение. а) По формуле (1.1) имеем 4(x -3)-2(y +2)+2(z -4)=0. Преобразуем его к виду (1.2): 4 x -2 y +8 z -48=0. Это - общее уравнение плоскости. Его можно сократить на 2: 2 x - y +4 z -24=0.
2) Написать различные уравнения плоскости:
а) проходящей через точку N (4; 2; -3) параллельно векторам 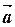 =(3; -1; 4),
=(3; -1; 4), 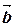 =(3; -4; 2);
=(3; -4; 2);
б) проходящей через точки N (5; -8; 3) параллельно векторам 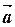 =(2; 3; -1),
=(2; 3; -1), 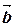 =(4; 1; -2);
=(4; 1; -2);
в) проходящей через точки N (2; -1; 3), M (3; -4; -2) и K (3; 2; 1);
г) проходящей через точки N (3; 2; -8), M (3; -5; 3) и K (2; 2; -3).
Решение. а) По формуле (1.3) имеем
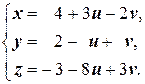
Получили параметрические уравнения плоскости.
Далее, по формуле (1.4) имеем
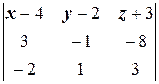 =0.
=0.
Раскроем определитель в левой части и приведём подобные:
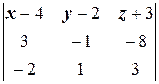 =5 x -15 y + z +32.
=5 x -15 y + z +32.
Таким образом, получаем общее уравнение плоскости: 5 x -15 y + z +32=0.
в) По формуле (1.5) имеем
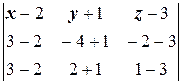 =0 Û
=0 Û 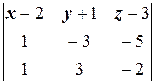 =0.
=0.
Осталось расписать определитель в правой части последнего уравнения и получить общее уравнение плоскости, что предоставляется читателю.
Напишем уравнение в параметрической форме. Для этого заметим, что векторы 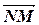 =(1; -3; -5) и
=(1; -3; -5) и 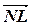 =(1; 3; -2) являются направляющими для данной плоскости. Поэтому по (2.3) имеем
=(1; 3; -2) являются направляющими для данной плоскости. Поэтому по (2.3) имеем
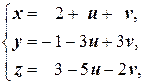
- параметрические уравнения плоскости.
Ответ: а) 2 x - y +4 z -24=0 - общее плоскости.
 2015-03-08
2015-03-08 1511
1511
