2.3.1. Введём на плоскости (в пространстве), где рассматриваются векторы, прямоугольную декартову систему координат. Отложим вектор  от начала координат:
от начала координат:  =
= 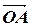 . Тогда координаты конца A вектора
. Тогда координаты конца A вектора  называются координатами вектора
называются координатами вектора  . Их будем обозначать через (ax, ay) на плоскости и через (ax, ay, az) - в пространстве (рис.2.4).
. Их будем обозначать через (ax, ay) на плоскости и через (ax, ay, az) - в пространстве (рис.2.4).

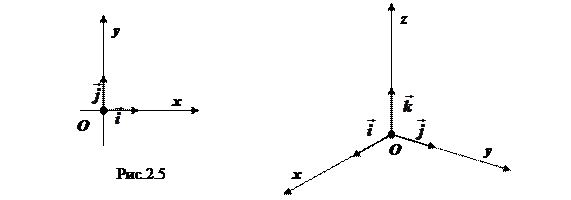
2.3.2. «Привяжем» реперы к системе координат так, чтобы направление  совпало с положительным направлением оси Ох, направление
совпало с положительным направлением оси Ох, направление  - с положительным направлением оси Оу и направление
- с положительным направлением оси Оу и направление  - с положительным направлением оси Оz (рис. 2.5). Тогда легко видеть, что если
- с положительным направлением оси Оz (рис. 2.5). Тогда легко видеть, что если  имеет координаты (ax, ay) в прямоугольной декартовой системе на плоскости и (ax, ay, az) - в пространстве, то
имеет координаты (ax, ay) в прямоугольной декартовой системе на плоскости и (ax, ay, az) - в пространстве, то  = ax
= ax  + ax
+ ax 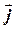 на плоскости и
на плоскости и  = ax
= ax  + ay
+ ay 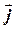 + az
+ az  в пространстве. Так что координаты
в пространстве. Так что координаты  в репере и в прямоугольной декартовой системе координат совпадают. Поэтому записи
в репере и в прямоугольной декартовой системе координат совпадают. Поэтому записи  =(ax, ax) и
=(ax, ax) и  =(ax, ay, az) одновременно означают, что
=(ax, ay, az) одновременно означают, что  имеет координаты (ax, ax) на плоскости и (ax, ay, az) в пространстве и такие же координаты в репере, соответственно на плоскости и в пространстве.
имеет координаты (ax, ax) на плоскости и (ax, ay, az) в пространстве и такие же координаты в репере, соответственно на плоскости и в пространстве.
2.3.4. Если вектор  =(ax, ax) (
=(ax, ax) ( =(ax, ay, az)) задан в прямоугольной декартовой системе координат на плоскости (в пространстве), то длину этого вектора можно вычислить по формуле |
=(ax, ay, az)) задан в прямоугольной декартовой системе координат на плоскости (в пространстве), то длину этого вектора можно вычислить по формуле |  |=
|= 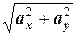 (|
(|  |=
|= 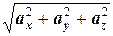 ).
).
 2015-03-08
2015-03-08 863
863








