3.1.1. Скалярным произведением векторов  и
и  называется число |
называется число |  |×|
|×|  |×cos(
|×cos(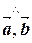 ). Векторы
). Векторы  и
и  называются сомножителями в скалярном произведении.
называются сомножителями в скалярном произведении.
Скалярное произведение векторов  и
и  обозначается через (
обозначается через ( ,
,  ). Таким образом, по определению
). Таким образом, по определению
( ,
,  )=|
)=|  |×|
|×|  |×cos(
|×cos(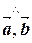 ) (3.1)
) (3.1)
3.1.2. Если  и
и  коллинеарны, то (
коллинеарны, то ( ,
,  )=±|
)=±|  |×|
|×|  |. При этом знак «+» берётся в случае, когда
|. При этом знак «+» берётся в случае, когда 
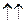
 , и «-» - когда
, и «-» - когда 
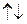
 . В частности,
. В частности, 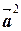 =(
=( ,
,  )=
)= 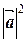 .
.
Наконец, векторы  и
и  ортогональны тогда и только тогда, когда их скалярное произведение равно 0: (
ортогональны тогда и только тогда, когда их скалярное произведение равно 0: ( ,
,  )=0.
)=0.
3.1.3. Теорема. Скалярное произведение векторов обладает следующими свойствами:
1о. Для любых векторов  и
и  имеет место равенство
имеет место равенство
( ,
,  )=(
)=( ,
,  ).
).
2о. Для любого числа a и любых векторов  и
и  имеют место равенства
имеют место равенства
(a  ,
,  )= a (
)= a ( ,
,  ),
),
( , a
, a  )= a (
)= a ( ,
,  ).
).
3о. Для любых векторов  ,
,  и
и  имеют место равенства
имеют место равенства
( +
+  ,
,  )=(
)=( ,
,  )+(
)+( ,
,  ),
),
( ,
,  +
+  )=(
)=( ,
,  )+(
)+( ,
,  ).
).
4о. Если  =(ax, ay, az),
=(ax, ay, az),  =(bx, by, bz), то
=(bx, by, bz), то
( ,
,  )= axbx + ayby + azbz. (3.2)
)= axbx + ayby + azbz. (3.2)
Аналогичное свойство справедливо и для векторов на плоскости (только будет отсутствовать слагаемое azbz). В частности, axbx + ayby + azbz =0 - условие ортогональности векторов  и
и  .
.
3.1.4. Свойства 2о и 3о обобщаются на любое число слагаемых в любом из сомножителей:
(a 1 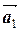 + a 2
+ a 2 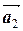 +…+ ak
+…+ ak 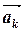 ,
,  )= a 1(
)= a 1(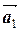 ,
,  )+ a 2(
)+ a 2(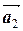 ,
,  )+…+ ak (
)+…+ ak (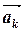 ,
,  ),
),
( , b 1
, b 1 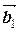 + b 2
+ b 2 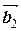 +…+ bk
+…+ bk 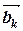 )= b 1(
)= b 1( ,
, 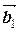 )+ b 2(
)+ b 2( ,
, 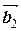 )+…+ bk (
)+…+ bk ( ,
, 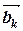 )
)
Аналогичное обобщение имеет место на любое число слагаемых в обоих сомножителях. Например,
(a  + b
+ b  , g
, g  + d
+ d  + e
+ e 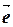 )=
)=
= ag ( ,
,  )+ bg (
)+ bg ( ,
,  )+ ad (
)+ ad ( ,
,  )+ bd (
)+ bd ( ,
,  )+ ae (
)+ ae ( ,
, 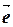 )+ be (
)+ be ( ,
, 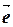 ).
).
3.1.5. Если известны координаты векторов  и
и  , то можно определить косинус cos(
, то можно определить косинус cos(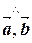 ) угла между ними, а по косинусу - и сам угол (
) угла между ними, а по косинусу - и сам угол (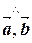 ). Действительно, для векторов в пространстве из (3.1) имеем
). Действительно, для векторов в пространстве из (3.1) имеем
cos(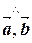 )=
)= 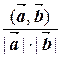 ,
,
куда подставляя (3.2) и |  |=
|= 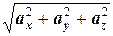 ,
,  =
= 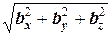 , получаем
, получаем
cos(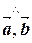 )=
)= 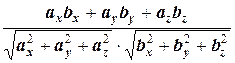 (3.3).
(3.3).
Аналогичная формула верна и для векторов на плоскости.
 2015-03-08
2015-03-08 460
460








