3.2.1. Векторным произведением векторов  и
и  называется вектор
называется вектор  , обладающий следующими свойствами:
, обладающий следующими свойствами:
1)  ^
^  ,
,  ^
^  ;
;
2) |  |=|
|=|  |×|
|×|  |×sin(
|×sin(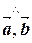 );
);
3) тройка ( ,
,  ,
,  ) - правая.
) - правая.
Векторное произведение векторов  и
и  обозначается через [
обозначается через [  ,
,  ] и
] и  ´
´  .
.
3.2.2. Свойство 3) определения векторного произведения векторов  и
и  выражает его геометрический смысл: Геометрический смысл векторного
выражает его геометрический смысл: Геометрический смысл векторного 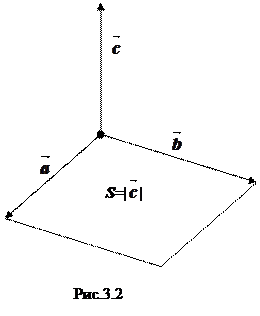 произведения заключается в том, что длина векторного произведения равна площади параллелограмма, натянутого на сомножители (рис.3.2).
произведения заключается в том, что длина векторного произведения равна площади параллелограмма, натянутого на сомножители (рис.3.2).
При этом  и
и  коллинеарны, тогда и только тогда, когда [
коллинеарны, тогда и только тогда, когда [  ,
,  ]=
]=  .
.
3.1.3. Теорема. Векторное произведение векторов обладает следующими свойствами:
1о. Для любых векторов  и
и  имеет место равенство
имеет место равенство
[  ,
,  ]=-[
]=-[  ,
,  ].
].
2о. Для любого числа a и любых векторов  и
и  имеют место равенства
имеют место равенства
[ a  ,
,  ]= a [
]= a [  ,
,  ],
],
[  , a
, a  ]= a [
]= a [  ,
,  ].
].
3о. Для любых векторов  ,
,  и
и  имеют место равенства
имеют место равенства
[  +
+  ,
,  ]=[
]=[  ,
,  ]+[
]+[  ,
,  ],
],
[  ,
,  +
+  ]=[
]=[  ,
,  ]+[
]+[  ,
,  ].
].
4о. Если  =(ax, ay, az),
=(ax, ay, az),  =(bx, by, bz), то
=(bx, by, bz), то
[  ,
,  ]=
]= 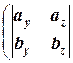 , -
, - 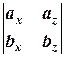 ,
, 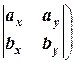 (3.4)
(3.4)
или, в виде разложения в системе орт
[  ,
,  ]=
]= 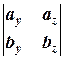
 -
- 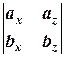
 +
+ 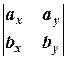
 (3.5)
(3.5)
3.2.4. Свойства 2о и 3о обобщаются на любое число слагаемых в любом из сомножителей:
[ a 1 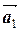 + a 2
+ a 2 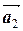 +…+ ak
+…+ ak 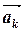 ,
,  ]= a 1[
]= a 1[ 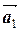 ,
,  ]+ a 2[
]+ a 2[ 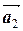 ,
,  ]+…+ ak [
]+…+ ak [ 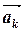 ,
,  ],
],
[  , b 1
, b 1 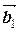 + b 2
+ b 2 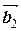 +…+ bk
+…+ bk 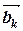 [= b 1[
[= b 1[  ,
, 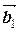 ]+ b 2[
]+ b 2[  ,
, 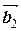 ]+…+ bk [
]+…+ bk [  ,
, 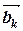 ]
]
Аналогичное обобщение имеет место на любое число слагаемых в обоих сомножителях. Например,
[ a  + b
+ b  , g
, g  + d
+ d  + e
+ e 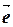 ]=
]=
= ag [  ,
,  ]+ bg [
]+ bg [  ,
,  ]+ ad [
]+ ad [  ,
,  ]+ bd [
]+ bd [  ,
,  ]+ ae [
]+ ae [  ,
, 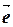 ]+ be [
]+ be [  ,
, 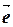 ].
].
3.2.5. Равенство (3.5) формально записывается в виде
[  ,
,  ]=
]= 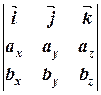 (3.6)
(3.6)
Формула (3.6) позволяет легко восстановить формулу (3.5) (при условии знания определителя 3-го порядка или его разложения по первой строке).
 2015-03-08
2015-03-08 440
440








