1) Вычислить площадь параллелограмма, построенного на векторах  и
и  , если:
, если:
а)  =2
=2  -3
-3  ,
,  =-
=-  +3
+3  , |
, |  |=2, |
|=2, |  |=3, (
|=3, (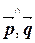 )=
)= 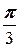 ;
;
б)  =-2
=-2  -4
-4  ,
,  =3
=3  -2
-2  , |
, |  |=1, |
|=1, |  |=4, (
|=4, (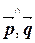 )=
)= 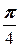 ;
;
в)  =
=  +5
+5  ,
,  =-2
=-2  -
-  , |
, |  |=2, |
|=2, |  |=4, (
|=4, (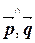 )=
)= 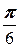 .
.
Решение. а) В силу геометрического смысла векторного произведения (3.2.2) площадь S параллелограмма, натянутого на векторы  и
и  , равна длине вектора [
, равна длине вектора [  ,
,  ], то есть S =|[
], то есть S =|[  ,
,  ]|. Найдём отдельно [
]|. Найдём отдельно [  ,
,  ]:
]:
[  ,
,  ]=[2
]=[2  -3
-3  , -
, -  +3
+3  ]
] 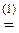 -2[
-2[  ,
,  ]+3[
]+3[  ,
,  ]+6[
]+6[  ,
,  ]-9[
]-9[  ,
,  ]
] 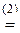
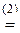 -3[
-3[  ,
,  ]+6[
]+6[  ,
,  ]=3[
]=3[  ,
,  ].
].
Поэтому S =|3[  ,
,  ]|=3|[
]|=3|[  ,
,  ]|=3|
]|=3|  |×|
|×|  |sin(
|sin(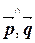 )=3×2×3×sin
)=3×2×3×sin 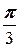 =9
=9  .
.
á(1) Воспользовались обобщением 3.2.4 свойств векторного произведения.
(2) Воспользовались свойствами [ 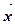 ,
, 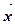 ] и [
] и [ 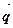 ,
, 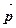 ]=-[
]=-[ 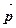 ,
,  ]ñ
]ñ
Ответ: а) S =9  .
.
2) Найти векторное произведение векторов  и
и  и его длину:
и его длину:
а)  =(3; -2; 4),
=(3; -2; 4),  =(2; -1; 3);
=(2; -1; 3);
б)  =(1; 2; -4),
=(1; 2; -4),  =(3; -5; 1);
=(3; -5; 1);
в) векторы  и
и  из упр 1.а),
из упр 1.а),  =(1; -1; 3),
=(1; -1; 3),  =(4; -2; 5);
=(4; -2; 5);
г)  =-3
=-3  +
+  ,
,  =4
=4  -2
-2  ,
,  =(2; 0; -1),
=(2; 0; -1),  =(2; 3; 6).
=(2; 3; 6).
Решение. а) По формуле (3.5) имеем
[  ,
,  ]=
]= 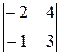
 -
- 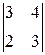
 +
+ 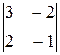
 =-2
=-2  -
-  +
+  ,
,
То есть [  ,
,  ]=-2
]=-2  -
-  +
+  . Далее |[
. Далее |[  ,
,  ]|=
]|= 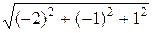 =
= 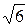 .
.
в) [  ,
,  ]=[2
]=[2  -3
-3  , -
, -  +3
+3  ]=3[
]=3[  ,
,  ] (см. решение упр. 1.а)) Далее,
] (см. решение упр. 1.а)) Далее,
[  ,
,  ]=
]= 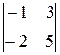
 -
- 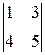
 +
+ 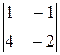
 =5
=5  +7
+7  +2
+2  .
.
Отсюда [  ,
,  ]=3(5
]=3(5  +7
+7  +2
+2  )=15
)=15  +21
+21  +6
+6  и |[
и |[  ,
,  ]|=
]|= 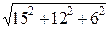 =
= 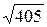 .
.
Ответ: а) [  ,
,  ]=-2
]=-2  -
-  +
+  , |[
, |[  ,
,  ]|=
]|= 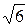 ;
;
в) [  ,
,  ]=15
]=15  +21
+21  +6
+6  , |[
, |[  ,
,  ]|=
]|= 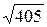 .
.
 2015-03-08
2015-03-08 1535
1535








