Смешанное произведение векторов и его свойства

3.3.1. Смешанным произведением векторов , и называется число, равное скалярному произведению ([ , ], ) вектора [ , ] (векторного произведения векторов и ) на вектор .

Смешанное произведение векторов , и обозначается через (, , ). Таким образом, по определению (, , )=([ , ], ).

Векторы , и называются сомножителями в смешанном произведении.

3.3.2. Теорема. Смешанное произведение векторов обладает следующими свойствами:

1^о. Для любых векторов , и имеет место равенство

(, , )=(, , )=(, , )=-(, , )=(, , )=-(, , ).

2^о. Для любого числа a и любых векторов , и имеют место равенства

(a , , )=(, a , )=(, , a ).

3^о. Для любых векторов , , и имеют место равенства

( + , , )=(, , )+(, , ),

(, + , )=(, , )+(, , ),

(, , + )=(, , )+(, , ).

4^о. Если =(a_x, a_y, a_z), =(b_x, b_y, b_z), =(с_x, с_y, с_z) то

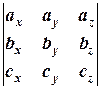(, , )= (3.7)

В частности, векторы , и компланарны тогда и только тогда, когда их смешанное произведение равно 0.

5^о. Если V - объём параллелепипеда, натянутого на векторы , , , то (, , )=± V, причём берётся знак «+», если тройка (, , ) - правая, знак «-» - если эта тройка - левая.

3.3.3. Свойства 2^о и 3^о обобщаются на любое число слагаемых в любом из сомножителей (как и соответствующие свойства скалярного и векторного произведений). Мы их приводить не будем. При желании читатель сам может сформулировать эти обобщения.

3.3.4. Из свойства 4^о вытекает геометрический смысл смешанного произведения: по абсолютной величине смешанное произведение векторов , , равно объёму V параллелепипеда, натянутого на эти векторы:

|(, , )|= V.

3.3.5. Наконец, из свойства 4^о также вытекает, что векторы , , образуют базис в пространстве тогда и только тогда, когда их смешанное произведение не равно 0.