1) Найти объём параллелепипеда, натянутого на векторы  ,
,  ,
,  ; выяснить, образуют ли эти векторы базис в пространстве:
; выяснить, образуют ли эти векторы базис в пространстве:
а)  =(3; -1; 2),
=(3; -1; 2),  =(2; 1; 1),
=(2; 1; 1),  =(1; -1; 2);
=(1; -1; 2);
б)  =(1; 2; 3),
=(1; 2; 3),  =(4; 5; 6),
=(4; 5; 6),  =(7; 8; 9);
=(7; 8; 9);
в)  =(1; -1; 1),
=(1; -1; 1),  =(2; 1; -1),
=(2; 1; -1),  =(1; 2; 3).
=(1; 2; 3).
Решение. а) По свойству 3.3.4 объём V параллелепипеда, натянутого на векторы  ,
,  ,
,  , можно вычислить по формуле V =|(
, можно вычислить по формуле V =|( ,
,  ,
,  )|. Так как по свойству 4о
)|. Так как по свойству 4о
( ,
,  ,
,  )=
)= 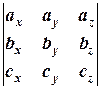 =
= 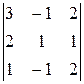 =6,
=6,
то V =6. В частности, по 3.3.5  ,
,  ,
,  образуют базис в пространстве.
образуют базис в пространстве.
2) Найти объём тетраэдра ABCD и длину её высоты, опущенной из вершины D:
а) A (-1; 2; -3), B (3; -2; 4), C (8; 1; 3), D (2; 4; 1);
б) A (-2; -2; 3), B (-3; 4; 2), C (3; 1; 3), D (3; -4; 1);
в) A (1; 4; -4), B (8; -1; -4), C (-5; -1; 4), D (-2; 3; 4).
Решение. а) Из школьного курса геометрии известно, что если тетраэдр и треугольная призма имеют одинаковые основание и высоту, то объёмы V тетр и V пр соответственно тетраэдра и призмы относятся как V тетр= 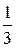 V пр. Отсюда вытекает, что V тетр=
V пр. Отсюда вытекает, что V тетр= 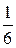 V пар, где V пар - объём параллелепипеда, натянутого на векторы
V пар, где V пар - объём параллелепипеда, натянутого на векторы  ,
,  ,
, 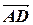 (рис.3.3). Имеем
(рис.3.3). Имеем  =(4, -4, 7),
=(4, -4, 7),  =(9, -1, 6),
=(9, -1, 6), 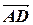 =(3, 2, 4),
=(3, 2, 4),
V пар= 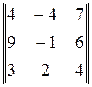 =|-16+126-72+21+144-48|=155.
=|-16+126-72+21+144-48|=155.
Поэтому V тетр= 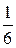 ×155=
×155= 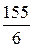 .
.
Для нахождения длины h высоты, опущенной из вершины D, найдём площадь основания, на которое она опущена: SABC = 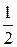 |[
|[  ,
,  ]|. Имеем
]|. Имеем
[  ,
,  ]=
]= 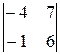
 -
- 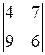
 +
+ 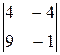
 =17
=17  -39
-39  +32
+32 
и |[  ,
,  ]|=
]|= 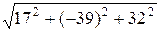 =
= 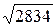 . Поэтому SABC =
. Поэтому SABC = 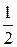
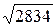 . Так как V пар=
. Так как V пар= 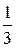 SABC × h, то h =
SABC × h, то h = 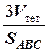 =
= 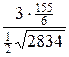 =
= 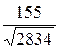 .
.
Ответ: V тетр= 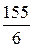 , h =
, h = 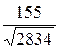 .
.
Приложения
Приложение 1. Варианты индивидуальных заданий
 2015-03-08
2015-03-08 1674
1674
