Данные для каждого варианта индивидуальных заданий приведены ниже. Во всех вариантах предлагается выполнить следующие задания:
1. Даны точки A и B своими координатами. Известно, что точка C делит отрезок AB в отношении l. Найти длину отрезка AB, координату точки C и координату середины D отрезка AB. Для точек A, B и С на прямой и плоскости сделать чертёж.
2. Точка A дана своими:
а) полярными; б) цилиндрическими; в) сферическими
координатами. Найти её прямоугольные координаты.
3. Найти расстояние между точками A и B, заданными своими:
а) полярными; б) цилиндрическими; в) сферическими
координатами.
4. Точка A задана своими координатами в прямоугольной системе координат Oxy. Система Oxy подвергается параллельному переносу, O ¢ - начало новой системы O ¢ x ¢ y ¢. Найти координаты точки A в новой системе.
5. Известны: прямоугольные координаты точки A в новой системе, которая получена параллельным переносом; координаты начала O ¢ в старой системе. Найти координаты A в старой системе.
6. Новая прямоугольная система Ox ¢ y ¢ получается поворотом вокруг начала О на угол a. Известны новые координаты точки А. Найти старые.
7. Новая прямоугольная система Ox ¢ y ¢ получается поворотом вокруг начала О на угол a. Известны старые координаты точки А. Найти новые. теме.
8. Найти геометрическое место точек, равноудалённых от точек A и B. теме.
9. См. ниже в соответствующем варианте.
10. Найти линейную зависимость между векторами  ,
,  ,
,  и
и  .
.
11. На плоскости даны векторы  и
и 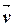 . Доказать, что они образуют базис на плоскости и найти координаты вектора
. Доказать, что они образуют базис на плоскости и найти координаты вектора  в этом базисе.
в этом базисе.
12. В пространстве даны векторы 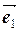 ,
, 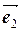 и
и 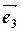 . Доказать, что они образуют базис в пространстве и найти координаты вектора
. Доказать, что они образуют базис в пространстве и найти координаты вектора  в этом базисе.
в этом базисе.
13. Векторы  и
и  взаимно перпендикулярны, вектор
взаимно перпендикулярны, вектор  образует с ними углы, равные a и b соответственно; зная длины векторов
образует с ними углы, равные a и b соответственно; зная длины векторов  ,
,  и
и  , вычислить скалярные произведения.
, вычислить скалярные произведения.
14. Найти вектор 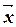 , если он перпендикулярен векторам
, если он перпендикулярен векторам  и
и  и удовлетворяет условию (
и удовлетворяет условию (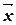 ,
,  )= d.
)= d.
15. Вычислить внутренние углы треугольника ABC и убедиться, что этот треугольник ¾ равнобедренный, если известны вектора  и
и 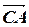 .
.
16. Найти косинус угла между векторами  и
и  , если известны координаты точек A, B и C.
, если известны координаты точек A, B и C.
17. Вычислить площадь параллелограмма, построенного на векторах  и
и  .
.
18. Даны векторы  ,
,  и
и  . Вычислить: а) векторное произведение векторов
. Вычислить: а) векторное произведение векторов  и
и  и его длину; б) образует ли тройка векторов (
и его длину; б) образует ли тройка векторов ( ,
,  ,
, 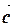 ) базис в пространстве?
) базис в пространстве?
19. Вычислить объём тетраэдра с вершинами в точках A 1, A 2, A 3, A 4 и его высоту, опущенную из вершины A 4 на грань A 1 A 2 A 3.
2. Данные по вариантам
Вариант 1
1. а) A (2), B (-4), l = 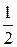 ; б) A (-2; 1), B (4; -1), l =
; б) A (-2; 1), B (4; -1), l = 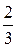 ;
;
в) A (3; -1; 4), B (-4; 1; 2), l = 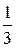 .
.
2. а) A 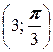 ; б) A
; б) A 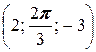 ; в) A
; в) A 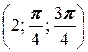 .
.
3. а) A 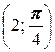 , B
, B 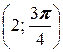 ; б) A
; б) A 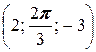 , B
, B 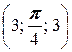 ;
;
в) A 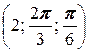 , B
, B 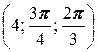 .
.
4. A (-2; 3), O ¢ (3, 2).
5. A (3; -2), O ¢ (3, 2).
6. a = 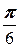 , A (3; -2).
, A (3; -2).
7. a = 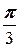 , A (3; -2).
, A (3; -2).
8. A (4; -2), B (3, 1).
9. Дан треугольник ABC, E, F и G ¾ середины AB, BC и AC соответственно. Выразить  ,
, 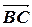 ,
,  через
через  =
= 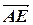 ,
,  =
= 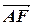 .
.
10.  =(0, 1, 1),
=(0, 1, 1),  =(1, 2, -1),
=(1, 2, -1),  =(2, 2, 1),
=(2, 2, 1),  =(1, 3, 5).
=(1, 3, 5).
11.  =(1, 3),
=(1, 3), 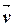 =(-1, 2),
=(-1, 2),  =(3, 4).
=(3, 4).
12. 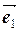 =(2; -1; -2),
=(2; -1; -2), 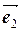 =(1; -1; 1),
=(1; -1; 1), 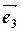 =(-1; 1; 2),
=(-1; 1; 2),  =(-1; 6; 3).
=(-1; 6; 3).
13. a = 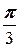 , b =
, b = 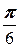 , |
, |  |=3, |
|=3, |  |=5, |
|=5, | 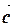 |=8, вычислить:
|=8, вычислить:
а) (3  -2
-2  ,
,  +3
+3  ); б) (2
); б) (2  +
+  -
-  )2.
)2.
14.  =(2, 3, -1),
=(2, 3, -1),  =(1, -2, 3),
=(1, -2, 3),  =2
=2  -
-  +
+  , d =-6.
, d =-6.
15.  =(2, 1, 2),
=(2, 1, 2), 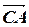 =(-3, 1, -4).
=(-3, 1, -4).
16. A (1, -2, 3), B (0, -1, 2), C (3, -4, 5).
17.  =
=  +2
+2  ,
,  =3
=3  -
-  , |
, |  |=1, |
|=1, |  |=2, (
|=2, (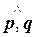 )=
)= 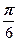 .
.
18.  =(2, 3, 1),
=(2, 3, 1),  =(-1, 0, -1),
=(-1, 0, -1), 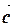 =(2, 2, 2).
=(2, 2, 2).
19. A 1(-4, 2, 6), A 2(2, -3, 0), A 3(-10, 5, 0), A 4(-5, 2, -4).
Вариант 2
1. а) A (-2), B (-4), l = 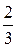 ; б) A (2; 1), B (-4; -1), l =
; б) A (2; 1), B (-4; -1), l = 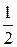 ;
;
в) A (2; -2; 4), B (-4; 3; 2), l = 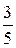 ;
;
2. а) A 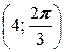 ; б) A
; б) A 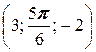 ; в) A
; в) A 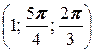 .
.
3. а) A 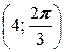 , B
, B 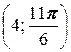 ; б) A
; б) A 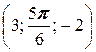 , B
, B 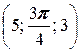 ;
;
в) A 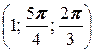 , B
, B 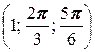 .
.
4. A (-2; -3), O ¢ (-3, 2).
5. A (3; 5), O ¢ (3, -1).
6. a = 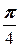 , A (-3; 5).
, A (-3; 5).
7. a = 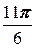 , A (4; -1).
, A (4; -1).
8. A (3; -3), B (-1, 4).
9. Дан треугольник ABC, E, F и G ¾ середины AB, BC и AC соответственно. Выразить  ,
, 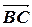 ,
,  через
через  =
= 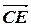 ,
,  =
= 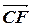 .
.
10.  =(
=(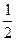 ,
, 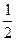 , 0),
, 0),  =(-1, 0, -3),
=(-1, 0, -3),  =(1, 1, -1),
=(1, 1, -1),  =(4, 2, 2).
=(4, 2, 2).
11.  =(2, -2),
=(2, -2), 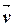 =(3, 2),
=(3, 2),  =(1, -6).
=(1, -6).
12. 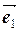 =(6; -1; -2),
=(6; -1; -2), 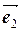 =(1; -2; -2),
=(1; -2; -2), 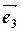 =(1; -1; 2),
=(1; -1; 2),  =(-1; 3; -2).
=(-1; 3; -2).
13. a = 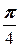 , b =
, b = 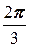 , |
, |  |=3, |
|=3, |  |=5, |
|=5, |  |=8, вычислить:
|=8, вычислить:
а) (3  +2
+2  , -
, -  +
+  +
+  ); б) (
); б) ( +
+  +
+  )2.
)2.
14.  =(2, 3, -1),
=(2, 3, -1),  =(1, -2, 3),
=(1, -2, 3),  =
=  -2
-2  +2
+2  , d =3.
, d =3.
15. 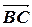 =(3, 1, -1),
=(3, 1, -1), 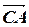 =(-4, -4, 2).
=(-4, -4, 2).
16. A (-1, -2, -3), B (0, 1, -2), C (-3, 6, 5).
17.  =3
=3  +
+  ,
,  =
=  -2
-2  , |
, |  |=4, |
|=4, |  |=1, (
|=1, (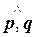 )=
)= 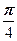 .
.
18.  =(3, 2, 1),
=(3, 2, 1),  =(2, 3, 4),
=(2, 3, 4),  =(3, 1, -1).
=(3, 1, -1).
19. A 1(-4, 2, 6), A 2(2, -3, 0), A 3(-10, 5, 0), A 4(-5, 2, -4).
Вариант 3
1. а) A (2), B (-3), l = 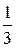 ; б) A (-2; -1), B (-4; 1), l =
; б) A (-2; -1), B (-4; 1), l = 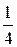 ;
;
в) A (-3; 1; 4), B (4; -3; -1), l = 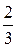 ;
;
2. а) A 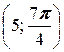 ; б) A
; б) A 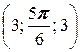 ; в) A
; в) A 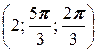 .
.
3. а) A 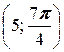 , B
, B 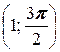 ; б) A
; б) A 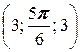 , B
, B 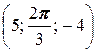 ;
;
в) A 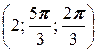 , B
, B 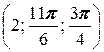 .
.
4. A (-1; 4), O ¢ (1, -3).
5. A (-2; 3), O ¢ (2, -3).
6. a =- 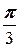 , A (4; 2).
, A (4; 2).
7. a = 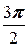 , A (-1; 2).
, A (-1; 2).
8. A (-3; 4), B (2, -1).
9. Дан треугольник ABC, E, F и G ¾ середины AB, BC и AC соответственно. Выразить  ,
, 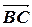 ,
,  через
через  =
= 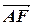 ,
,  =
= 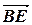 .
.
10.  =(3, 1, -1),
=(3, 1, -1),  =(0, 2, -3),
=(0, 2, -3),  =(-3, 3, -3),
=(-3, 3, -3),  =(-3, 7, -5).
=(-3, 7, -5).
11.  =(5, 0),
=(5, 0), 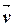 =(1, -2),
=(1, -2),  =(4, -2).
=(4, -2).
12. 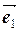 =(-3; 2; -2),
=(-3; 2; -2), 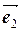 =(1; -1; 4),
=(1; -1; 4), 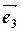 =(2; -2; 2),
=(2; -2; 2),  =(1; 3; -4).
=(1; 3; -4).
13. a = 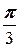 , b =
, b = 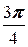 , |
, |  |=2, |
|=2, |  |=6, |
|=6, |  |=3, вычислить:
|=3, вычислить:
а) (2  +3
+3  ,
,  +
+  +4
+4  ); б) (3
); б) (3  -4
-4  -
-  )2.
)2.
14.  =(2, 3, -1),
=(2, 3, -1),  =(1, -2, 3),
=(1, -2, 3),  =2
=2  +3
+3  -2
-2  , d = -3.
, d = -3.
15.  =(3, 3, -2),
=(3, 3, -2), 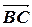 =(1, 2, -1).
=(1, 2, -1).
16. A (3, 3, -1), B (5, 5, -2), C (4, 1, 1).
17.  =
=  -3
-3  ,
,  =
=  +2
+2  , |
, |  |=3, |
|=3, |  |=2, (
|=2, (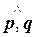 )=
)= 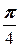 .
.
18.  =(1, 5, 2),
=(1, 5, 2),  =(-1, 1, -1),
=(-1, 1, -1),  =(1, 1, 1).
=(1, 1, 1).
19. A 1(7, 2, 4), A 2(7, -1, -2), A 3(3, 3, 1), A 4(-4, 2, 1).
Вариант 4
1. а) A (3), B (-2), l = 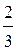 ; б) A (-1; 2), B (-3; -1), l =
; б) A (-1; 2), B (-3; -1), l = 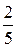 ;
;
в) A (3; -1; 3), B (4; 1; -3), l = 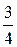 ;
;
2. а) A 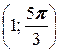 ; б) A
; б) A 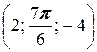 ; в) A
; в) A 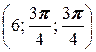 .
.
3. а) A 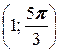 , B
, B 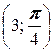 ; б) A
; б) A 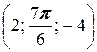 , B
, B 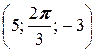 ;
;
в) A 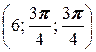 , B
, B 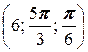 .
.
4. A (-1; 5), O ¢ (-2, 3).
5. A (2; 5), O ¢ (3, -2).
6. a = 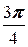 , A (-3; 4).
, A (-3; 4).
7. a =- 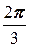 , A (3; -5).
, A (3; -5).
8. A (3; -5), B (4, 8).
9. Дан треугольник ABC, E, F и G ¾ середины AB, BC и AC соответственно. Выразить  ,
, 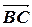 ,
,  через
через  =
= 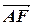 ,
,  =
= 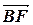 .
.
10.  =(
=(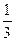 , -
, - 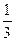 , 1),
, 1),  =(
=(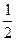 , 0, -1),
, 0, -1),  =(2, 3, -1),
=(2, 3, -1),  =(4, -1, 6).
=(4, -1, 6).
11.  =(4, -2),
=(4, -2), 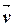 =(1, 2),
=(1, 2),  =(4, -2).
=(4, -2).
12. 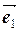 =(2; -7; 1),
=(2; -7; 1), 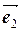 =(-1; 3; 3),
=(-1; 3; 3), 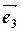 =(4; -1; 4),
=(4; -1; 4),  =(-7; 3; -1).
=(-7; 3; -1).
13. a = 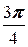 , b =
, b = 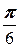 , |
, |  |=7, |
|=7, |  |=1, |
|=1, |  |=3, вычислить:
|=3, вычислить:
а) (2  -3
-3  ,
,  +
+  -3
-3  ); б) (-2
); б) (-2  +
+  -
-  )2.
)2.
14.  =(2, 3, -1),
=(2, 3, -1),  =(1, -2, 3),
=(1, -2, 3),  =3
=3  -5
-5  +3
+3  , d =2.
, d =2.
15.  =(1, -1, -2),
=(1, -1, -2), 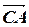 =(-2, -1, 1).
=(-2, -1, 1).
16. A (-1, 2, -3), B (3, 4, -6), C (1, 1, -1).
17.  =3
=3  -2
-2  ,
,  =
=  +5
+5  , |
, |  |=4, |
|=4, |  |=2, (
|=2, (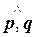 )=
)= 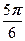 .
.
18.  =(1, -1, -3),
=(1, -1, -3),  =(3, 2, 1),
=(3, 2, 1),  =(2, 3, 4).
=(2, 3, 4).
19. A 1(2, 1, 4), A 2(-1, 5, -2), A 3(3, 3, 1), A 4(-4, 2, 1).
Вариант 5
1. а) A (-3), B (4), l = 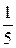 ; б) A (-2; -3), B (-2; -1), l =
; б) A (-2; -3), B (-2; -1), l = 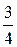 ;
;
в) A (2; -1; 4), B (-7; 1; -2), l = 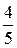 .
.
2. а) A 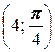 ; б) A
; б) A 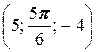 ; в) A
; в) A 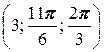 .
.
3. а) A 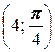 , B
, B 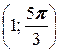 ; б) A
; б) A 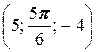 , B
, B 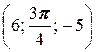 ;
;
в) A 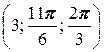 , B
, B  .
.
4. A (4; -2), O ¢ (-2, 8).
5. A (-3; 2), O ¢ (3, -2).
6. a = 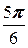 , A (4; -8).
, A (4; -8).
7. a =- 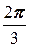 , A (3; -4).
, A (3; -4).
8. A (-4; 4), B (-3, 5).
9. Дан треугольник ABC, E, F и G ¾ середины AB, BC и AC соответственно. Выразить  ,
, 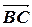 ,
,  через
через  =
= 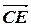 ,
,  =
= 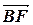 .
.
10.  =(5, 4, 2),
=(5, 4, 2),  =(5, 4, 3),
=(5, 4, 3),  =(5, 4, 1),
=(5, 4, 1),  =(-5, -4, 2).
=(-5, -4, 2).
11.  =(3, 1),
=(3, 1), 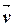 =(-1, 3),
=(-1, 3),  =(3, -1).
=(3, -1).
12. 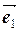 =(4; -4; -2),
=(4; -4; -2), 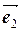 =(1; -6; -1),
=(1; -6; -1), 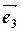 =(3; -1; -2),
=(3; -1; -2),  =(3; 3; -6).
=(3; 3; -6).
13. a = 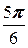 , b =
, b = 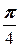 , |
, |  |=3, |
|=3, |  |=1, |
|=1, |  |=4, вычислить:
|=4, вычислить:
а) ( -
-  +2
+2  ,
,  -3
-3  ); б) (
); б) (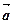 +2
+2  -3
-3  )2.
)2.
14.  =(2, 3, -1),
=(2, 3, -1),  =(1, -2, 3),
=(1, -2, 3),  =6
=6 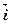 +
+ 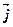 -7
-7 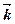 , d =5.
, d =5.
15. 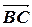 =(-1, -3, 2),
=(-1, -3, 2),  =(2, -2, 4).
=(2, -2, 4).
16. A (-4, -2, 0), B (-1, -2, 4), C (3, -2, 1).
17.  =
=  -2
-2  ,
,  =2
=2  +
+  , |
, |  |=2, |
|=2, |  |=3, (
|=3, (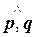 )=
)= 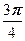 .
.
18.  =(3, 3, 1),
=(3, 3, 1),  =(1, -2, 1),
=(1, -2, 1),  =(1, 1, 1).
=(1, 1, 1).
19. A 1(0, -1, -1), A 2(-2, 3, 5), A 3(1, -5, -9), A 4(-1, -6, 3).
Вариант 6
1. а) A (2), B (0), l = 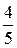 ; б) A (2; 1), B (-7; -1), l =
; б) A (2; 1), B (-7; -1), l = 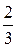 ;
;
в) A (7; -1; 4), B (-4; 6; 2), l = 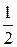 ;
;
2. а) A 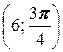 ; б) A
; б) A 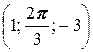 ; в) A
; в) A 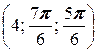 .
.
3. а) A 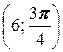 , B
, B 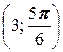 ; б) A
; б) A 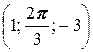 , B
, B 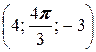 ;
;
в) A 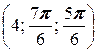 , B
, B 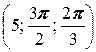 .
.
4. A (1; -8), O ¢ (4, -2).
5. A (2; -4), O ¢ (-4, 3).
6. a =- 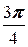 , A (13; -2).
, A (13; -2).
7. a = 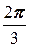 , A (10; -1).
, A (10; -1).
8. A (-1; -2), B (-3, 1).
9. Дан треугольник ABC, E, F и G ¾ середины AB, BC и AC соответственно. Выразить  ,
, 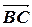 ,
,  через
через  =
= 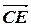 ,
,  =
= 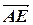 .
.
10.  =(2, -5, 1),
=(2, -5, 1),  =(4, 1, 5),
=(4, 1, 5),  =(2, 3, -3),
=(2, 3, -3),  =(3, -1, -6).
=(3, -1, -6).
11.  =(6, -3),
=(6, -3), 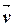 =(1, 4),
=(1, 4),  =(6, -1).
=(6, -1).
12. 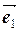 =(-1; -10; 3),
=(-1; -10; 3), 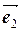 =(2; 7; -1),
=(2; 7; -1), 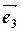 =(-2; 1; 4),
=(-2; 1; 4),  =(-2; 12; 2).
=(-2; 12; 2).
13. a = 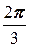 , b =
, b = 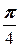 , |
, |  |=3, |
|=3, |  |=3, |
|=3, |  |=2, вычислить:
|=2, вычислить:
а) (3  +2
+2  , 3
, 3  -2
-2  ); б) (-3
); б) (-3  +
+  -
-  )2.
)2.
14.  =(2, 3, -1),
=(2, 3, -1),  =(1, -2, 3),
=(1, -2, 3),  =4
=4  -2
-2  -5
-5  , d =1.
, d =1.
15. 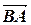 =(-1, -3, -1),
=(-1, -3, -1), 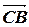 =(-2, 4, 2).
=(-2, 4, 2).
16. A (5, 3, -1), B (5, 2, 0), C (6, 4, -1).
17.  =
=  +3
+3  ,
,  =3
=3  -
-  , |
, |  |=3, |
|=3, |  |=2, (
|=2, (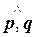 )=
)= 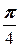 .
.
18.  =(3, 1, -1),
=(3, 1, -1),  =(-2, -1, 0),
=(-2, -1, 0),  =(5, 2, -1).
=(5, 2, -1).
19. A 1(-1, -5, 2), A 2(-6, 0, -3), A 3(3, 6, -3), A 4(-10, 6, 7).
Вариант 7
1. а) A (0), B (-4), l = 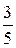 ; б) A (-6; 1), B (4; -10), l =
; б) A (-6; 1), B (4; -10), l = 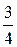 ;
;
в) A (3; -1; 0), B (-4; 10; 2), l = 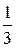 ;
;
2. а) A 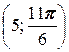 ; б) A
; б) A 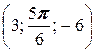 ; в) A
; в) A 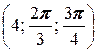 .
.
3. а) A 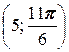 , B
, B 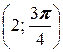 ; б) A
; б) A 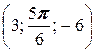 , B
, B 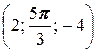 ;
;
в) A 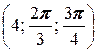 , A
, A 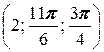 .
.
4. A (3; -9), O ¢ (1, -1).
5. A (2; 5), O ¢ (-6, 3).
6. a = 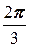 , A (3; -12).
, A (3; -12).
7. a =- 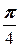 , A (-1; 2).
, A (-1; 2).
8. A (0; -2), B (-4, -2).
9. Дан треугольник ABC, E, F и G ¾ середины AB, BC и AC соответственно. Выразить  ,
, 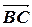 ,
,  через
через  =
= 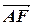 ,
,  =
= 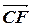 .
.
10.  =(3, -3, -1),
=(3, -3, -1),  =(6, -2, 5),
=(6, -2, 5),  =(1, -1, -4),
=(1, -1, -4),  =(6, -2, 1).
=(6, -2, 1).
11.  =(4, -2),
=(4, -2), 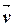 =(-1, -1),
=(-1, -1),  =(3, -2).
=(3, -2).
12. 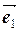 =(-1; -4; 3),
=(-1; -4; 3), 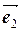 =(-2; 1; -3),
=(-2; 1; -3), 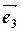 =(-2; 1; -5),
=(-2; 1; -5),  =(-2; 6; -2).
=(-2; 6; -2).
13. a = 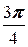 , b =
, b = 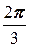 , |
, |  |=3, |
|=3, |  |=2, |
|=2, |  |=4, вычислить:
|=4, вычислить:
а) (3  +
+  ,
,  +2
+2  -3
-3  ); б) (2
); б) (2  -2
-2  +3
+3  )2.
)2.
14.  =(2, 3, -1),
=(2, 3, -1),  =(1, -2, 3),
=(1, -2, 3),  =
=  +
+  -3
-3  d = -4.
d = -4.
15.  =(3, 2, -1),
=(3, 2, -1), 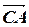 =(-1, 1, 2).
=(-1, 1, 2).
16. A (-3, -7, -5), B (0, -1, -2), C (2, 3, 0).
17.  =2
=2  -2
-2  ,
,  =
=  +3
+3  , |
, |  |=3, |
|=3, |  |=2, (
|=2, (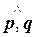 )=
)= 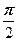 .
.
18.  =(4, 3, 1),
=(4, 3, 1),  =(1, -2, 1),
=(1, -2, 1),  =(2, 2, 2).
=(2, 2, 2).
19. A 1(5, 2, 0), A 2(2, 5, 0), A 3(1, 2, 4), A 4(-1, 1, 1).
Вариант 8
1. а) A (0), B (-2), l = 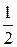 ; б) A (2; 1), B (0; -1), l =
; б) A (2; 1), B (0; -1), l = 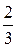 ;
;
в) A (3; -1; 0), B (-1; 1; 2), l = 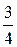 ;
;
2. а) A 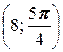 ; б) A
; б) A 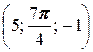 ; в) A
; в) A 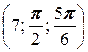 .
.
3. а) A 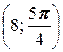 , B
, B 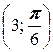 ; б) A
; б) A 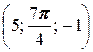 , B
, B 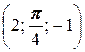 ;
;
в) A 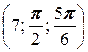 , B
, B 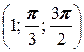 .
.
4. A (-4; 1), O ¢ (4, -2).
5. A (4; -5), O ¢ (-3, -4).
6. a = 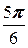 , A (4; -3).
, A (4; -3).
7. a =- 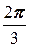 , A (3; -8).
, A (3; -8).
8. A (14; -2), B (3, 11).
9. Дан треугольник ABC, E, F и G ¾ середины AB, BC и AC соответственно. Выразить
|
|
 2015-03-08
2015-03-08 611
611







