2015-03-08
409
3.2.1. Определение. Пусть W ={1, 2, …, n }. Перестановкой множества W называется некоторый установленный порядок элементов из W: (i 1, i 2, …, in). Если в перестановке (i 1, …, is, …, it, …, in) is > it, то пара (is, it) называется инверсией перестановки (i 1, …, is, …, it, …, in). Число инверсий в перестановке (i 1, i 2, …, in) обозначается через [ i 1, i 2, …, in ].
3.2.2. Определение. Пусть дана квадратная матрица A =(aij) n ´ n. Определителем матрицы A называется алгебраическая сумма произведений элементов матрицы A, взятых в точности по одному из каждой строки и каждого столбца. При этом знаки слагаемых берутся по следующему правилу: если элементы матрицы в произведении идут в порядке следования номеров строк ¾ 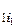a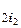 
a 
… a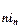 
, то со знаком «+» это слагаемое берётся в том случае, если перестановка (i 1, i 2, …, in) номеров столбцов чётная, и со знаком «-» ¾ если эта перестановка нечётная.
Определитель матрицы обозначается через
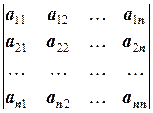
или, кратко, через det A.
3.2.3. Отметим некоторые свойства определителей:
1о. Если поменять местами любые две строки или два столбца определителя, то определитель изменит знак на противоположный, а по абсолютной величине не изменится.
|
|
|
2о. Если все элементы строки или столбца определителя умножить на один и тот же элемент a поля F, то определитель умножится на a. В частности, из строки или столбца можно вынести знак «-».
3о. Определитель не меняется, если ко всем элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на один и тот же элемент a поля F. В частности, определитель не меняется, если из элементов строки (столбца) вычесть соответствующие элементы другой строки (столбца), умноженные на один и тот же элемент a поля F.
4о. Определитель «треугольного» вида
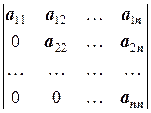
равен произведению диагональных элементов a 11 a 22… ann.
3.2.4. Определение. Пусть дана матрица A. Определитель k -го порядка, составленный из элементов матрицы A, стоящих на пересечении каких-либо k строк и k столбцов, называется миноромk - го порядка матрицы A.
Если A ¾ квадратная матрица размерности n ´ n, M ¾ некоторый минор k -го порядка, то у A можно рассматривать минор M ¢ порядка n - k, составленный из элементов, стоящих на пересечении строк и столбцов, которые не входят в минор M. Этот минор называется дополнительным минором кM. В частности, отдельно взятый элемент aij квадратной матрицы A =(aij) n ´ n является минором 1-го порядка, а его дополнительный минор ¾ минором n -1-го порядка. Он обозначается через Mij и называется минором элементаaij.
Алгебраическим дополнением минора M называется (-1)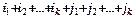 
M ¢, где i 1, i 2, …, ik ¾ номера строк, j 1, j 2, …, jk ¾ номера столбцов, на которых расположен минор M. В частности, алгебраическое дополнение элемента aij квадратной матрицы A =(aij) n ´ n (или его определителя) ¾ это Aij =(-1) i + jMij.
|
|
|
3.2.5. Отметим ещё несколько дальнейших свойств определителей:
5о. Пусть в определителе D произвольно выбраны k строк (или k столбцов). Тогда сумма произведений всех миноров k - го порядка, содержащихся в выбранных k строках, на их алгебраические дополнения равна определителю D (теорема Лапласа).
6о. Определитель равен сумме произведений элементов i - го столбца (i - й строки) на их алгебраические дополнения:
det A = a 1 i A 1 i + a 2 i A 2 i +…+ ani Ani (det A = ai 1 Ai 1+ ai 2 Ai 2+…+ ain Ain).
7о. Сумма произведений элементов i -го столбца (i -й строки) определителя на алгебраические дополнения соответствующих элементов другого столбца (строки) равна нулю:
a 1 i A 1 j + a 2 i A 2 j +…+ ani Anj =0 (ai 1 Aj 1+ ai 2 Aj 2+…+ ain Ajn =0).
