Измерение связи между явлениями. Коэффициент корреляции

Явления в природе и обществе находятся во взаимосвязи. Раз­личают две формы связи: функциональную и корреляционную.

Функциональная связь означает строгую зависи­мость явлений, т.е. определенному значению признака соответст­вует одно или несколько строго определенных значений другого.

Функциональные связи известны в физике: закон Ньютона о зависимости между силой действия F и ускорением а тела с массой m (F = ma); закон Ома о зависимости между напряжением U и силой тока I с сопротивлением R (U = IR); степень расширения тела определяется температурой нагре­вания; скорость свободно падающего тела зависит от величины ус­корения, силы тяжести и времени падения.

В клинической медицине, биологии, а также в социально-гиги­енических исследованиях зависимости носят характер корреляцион­ной (статистической) связи.При корреляционной связи значению каждой средней величины одного признака соответствует множество случайных значений друго­го взаимосвязанного с ним признака. Например:

- Вес человека, при прочих равных, зависит в основном от его роста. Однако по­мимо роста на величину веса влияют и другие факторы: питание, сос­тояние здоровья и т.д. Поэтому у лиц одинакового роста относи­тельно редко встречаются одни и те же величины веса, обычно вес варьирует в определенных пределах.

- Между уровнем температуры тела человека и числом сердеч­ных сокращений также существует определенная зависимость. Однако при одинаковой температуре тела у различных людей наблюдаются индивидуальные колебания частоты сердечных сокращений, варьирую­щие вокруг своей средней.

Окончательное решение вопроса о том, имеется ли в действительности эта связь, возможно после изучения природы явле­ний. Только качественный анализ позволяет установить наряду с на­личием еще и характер связи, т.е. определить представляет ли эта связь результат причинной зависимости одного явления от другого или их взаимной зависимости, либо оба явления зависят от како­го-то третьего.

При наличии действительной связи, установленной на основе конкретного анализа, статистика дает возможность измерить силу этой связи и установить степень зави­симости между изучаемыми явлениями.

Одним из способов измерения связи является вычисление коэф­фициента корреляции. Коэффициент корреляции одним числом измеряет силу связи между изучаемыми явлениями, а знак дает представление о ее направле­нии.

При положительной (прямой) связи, когда из­менение одного какого-либо явления идет в том же направлении, что и другого (например: рост экономической обеспеченности и улучшение питания населения), коэффициент корреляции может принимать любое значение в пределах от 0 до + 1.

В случае отрицательной (обратной) связи, когда изменение одного из изучаемых явлений сопровождается изменением другого в обратном направлении (например: снижение заболеваемости полиомиелитом по мере увеличения числа прививок против этой болезни), коэффициент корреляции выражается отрицательным числом и соответственно нахо­дится в пределах от 0 до (-1).

Чем ближе величина коэффициента корреляции к 1, тем соответственно сильнее (теснее) измеряемая им прямая или обратная связь. Коэффициент корреляции, равный 0, говорит о полном отсутствии связи.

Оценка размеров корреляции может производиться по следующей схеме:

Таблица 7.1

Оценка корреляции	Величина коэффициента корреляции при наличии:
прямой связи	обратной связи
Малая (слабая)	0 – 0,29	0 – (- 0,29)
Средняя (умеренная)	0,3 – 0,69	(-0,3) – (-0,69)
Большая (сильная)	0,7 - 1	(-0,7) – (- 1)

Коэффициент корреляции может быть вычислен методом квадра­тов, методом рангов.

Схема вычисления коэффициента корреляции по методу квадратов (метод Пирсона).

Таблица 7.2

Схема вычисления коэффициента корреляции методом квадратов

между среднемесячной температурой воздуха и числом детей в возрасте до 1 года, умерших от острых кишечных инфекций

Месяц года	Средняя температура воздуха (Со) (x)	Среднее количество детей, умерших от острых кишечных инфекций (в день) (y)	dx	dy	dx2	dy2	dx · dy
Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь		5,0 5,5 6,2 5,4 6,5 9,6 11,2 15,3 14,9 13,0 7,0 6,6	- 4,9 - 7,9 - 5,9 - 1,9 5,1 7,1 8,1 7,1 5,1 - 0,9 - 3,9 - 6,9	- 3,8 - 3,3 - 2,6 - 3,4 - 2,3 0,8 2,4 6,5 6,1 4,2 - 1,8 - 2,6	24,01 62,41 34,81 3,61 26,01 50,41 65,61 50,41 26,01 0,81 15,21 47,61	14,44 10,89 6,76 11,56 5,29 0,64 5,76 42,25 37,21 17,64 3,24 6,76	18,62 26,07 15,34 6,46 - 11,73 5,68 19,44 46,15 31,11 - 3,78 7,02 17,94
n = 12	Σ = 119,0 Мх = 9,9	Σ= 105,2 Му = 8,8			Σ=406,92	Σ=162,44	Σ=178,32

Последовательность расчета коэффициента корреляции методом квадратов:

1.Расчет средних М_х и М_y для рядов «х» и «y».

2.Вычисление отклонений каждой варианты ряда «х» и ряда «y» от их средних М_х и М_y.

3.Возведение отклонений d_x и d_y в квадрат.

4.Вычисление произведения d_x · d_y

5.Определение сумм d_x², d_y² и d_x · d_y.

6.Вычисление коэффициента корреляции по формуле:

Σ d_x · d_y

r_xy = ------------------

Σ d_x² · d_y²

178,32

r_xy = ---------------------- = + 0,7

406,92 · 162,44

7.Определение направления и силы связи (см. таблицу 7.1).

8.Расчет ошибки коэффициента корреляции по формуле:

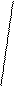
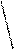1 – r²_xy

m_r = -------------

N - 2

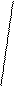
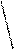1 – 0,49 0,51

m_r = ------------- = -------- = 0,226

12 - 2 10

9.Оценка достоверности коэффициента корреляции.

r_xy 0,7

t = ---------- = ------- = 3,1

m_r 0,226

Коэффициент корреляции достоверен, если он превышает свою ошибку в 3 и более раз.

Заключение: с достаточной для медицинских исследований надежностью, можно утверждать, что между среднемесячной температурой воздуха и числом детей в возрасте до 1 года, умерших от острых кишечных инфекций, существует прямая сильная корреляционная связь.

Кроме вычисления коэффициента корреляции по методу квадратов можно использовать вычисление коэффициента корреляции рангов по методу Спирмена (ρ).

Схема вычисления коэффициента корреляции методом рангов.

Таблица 7.3

Схема вычисления коэффициента корреляции методом рангов между возрастом студентов медицинского университета и их массой тела

Порядковый номер студента	Возраст (в годах) (х)	Масса тела (в кг) (у)	Ранги по возрасту (х1)	Ранги по массе тела (у1)	D	d2
			2,5 2,5 7,5 7,5 7,5 7,5		- 1,5 0,5 - 2 3,5 - 1,0 0,5 - 3,0 - 1,5 - 2,5	2,25 0,25 4,0 12,25 0,25 9,0 2,25 6,25
n = 10						Σ= 37,5

Последовательность расчета коэффициента корреляции методом рангов:

1.Составление рядов парных признаков х и y.

2.Замена каждой величины признака ранговым (порядковым) но­мером - х₁ и y₁.

При обозначении показателей рангами, начинают с меньшего (или с большего) в обоих рядах. Если отдельные показатели ряда встречаются несколько раз (например, 22; 23; 24), ранги проставляются следующим образом: возраст 22 года – встречается дважды, занимая по величине 2 и 3 ранговые места, поэтому порядковые номера в этом случае будут равны полусумме занимаемых этим возрастом мест - (2 + 3): 2 = 2,5, то есть против каждого показателя возраста 22 года проставляется ранг 2,5. Возраст 23 года встречается 3 раза, занимая 4, 5 и 6 ранговые места. Ранги для возраста 23 года будут равны: (4 + 5 + 6): 3 = 5, то есть против каждого показателя возраста 23 года проставляется ранг 5 и т.д.

3.Определение разности рангов d = x₁ - y₁.

4.Возведение в квадрат разности рангов - d².

5.Получение суммы квадратов разности рангов Σd².

6.Вычисление коэффициента ранговой корреляции по формуле:

6 · Σd²

ρ_xy = 1 - ---------------

n (n² – 1)

6 - постоянный коэффициент,

n - число наблюдений.

6 · 37,5 225

ρ_xy = 1 - --------------- = 1 - ------- = 1 – 0,2 = + 0,8

10 (10² – 1) 990

7.Определение направления и силы связи (см. таблицу 7.1).

8.Расчет ошибки коэффициента ранговой корреляции m_ρ по фор­муле:

1- ρ²_xy

m_ρ = -----------------

N - 2

1- 0,64

m_ρ = ----------------- = 0,045 = 0,2

10 - 2

9.Расчет критерия t и оценка достоверности коэффициента корреляции:

ρ_xy 0,8

t = ---------- = --------- = 4

m_ρ 0,2

Заключение: с достаточной для медицинских исследований надежностью, можно утверждать, что между возрастом студентов медицинского университета и их массой тела, существует прямая сильная корреляционная связь.

Метод Спирмена имеет некоторые преимущества перед методом Пирсона.

1. Метод Спирмена можно использовать при открытых значениях вариант (< 20; > 15 и т.д.).

2. Метод Спирмена можно использовать, если нет возможности измерить числовые значения вариант. Например, если нужно установить есть ли связь между ростом и весом у студентов в аудитории, в которой нет измерительных приборов. Можно проранжировать (построить) студентов по росту и весу. Метод Пирсона в этом случае не применим.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Какие виды связи существуют между явлениями и признаками?

2.Чем отличается корреляционная зависимость от функциональ­ной? Приведите примеры.

3.Что такое прямая и обратная связь?

4.Какие значения коэффициента корреляции указывают на нали­чие «слабой», «средней» и «сильной» связи?

5. Назовите методы вычисления коэффициента корреля­ции?

6.Какова формула определения коэффициента корреляции по ме­тоду квадратов (Пирсона)?

7.Какова последовательность расчета коэффициента корреляции по методу квадратов?

8.Какова формула расчета ошибки коэффициента корреляции по методу квадратов?

9.Какова формула определения коэффициента корреляции по ме­тоду рангов (Спирмена)?

10.Какова последовательность расчета коэффициента корреляции рангов?

11.Какова формула расчета ошибки коэффициента ранговой кор­реляции?

12.Как определить достоверность коэффициента корреляции?

ТЕСТЫ