Правило сложения дисперсий

Если изучаемая совокупность разделена на группы, то можно рассчитать:

1. Общую дисперсию исходной совокупности ( )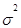

,

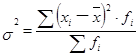где х_i – индивидуальные значения признака ( варианты) исходной совокупности;

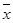– общая средняя величина исходной совокупности;

f_i – частоты исходной совокупности.

2. Межгрупповую дисперсию ( )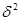

,

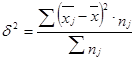где 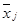– групповые средние величины;

n_j – численность единиц в j -й группе.

3. Внутригрупповые дисперсии ( )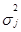

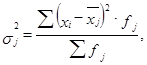
где f_j – частоты в каждой j -й группе.

4. Среднюю из внутригрупповых дисперсий по формуле

.

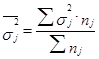Правило сложения дисперсий состоит в том, чтообщая дисперсия исходной совокупности равна сумме межгрупповой и средней из внутригрупповых дисперсий, т. е.

.

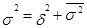Эмпирический коэффициент детерминации( 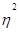) показывает долю общей вариации изучаемого признака, обусловленную вариацией группировочного признака

= .

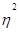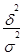Эмпирическое корреляционное отношение характеризует влияние группировочного признака на вариацию результативного признака

.

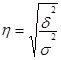Если 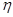= 0, то группировочный признак не влияет на результативный признак, если 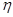= 1, то результативный признак полностью зависит от группировочного признака.