2015-03-08
644
Изменение частот в вариационных рядах называют закономерностями распределения. Кривая распределения – графическое изображение в виде непрерывной линии изменения частот в вариационном ряду.
Уравнение нормальной кривой имеет следующий вид:
у (t) =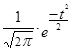 
,
где у (t) – ордината кривой нормального распределения;
t – нормированное отклонение, равное t =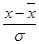 
;
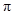– число 
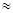3,1415;
e – число 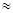2,7182.
Различают следующие виды кривых распределения:
– одновершинные (симметричные и асимметричные);
– многовершинные.
При симметричном распределении частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой, т. е.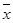 
= 
= 
.
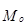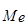Для сравнительного изучения асимметрии распределений вычисляют относительный показатель асимметрии (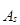 
) по формулам
= 
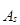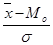или =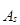 
.
При правосторонней асимметрии <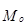 
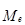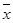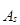< , > 0.
При левосторонней асимметрии 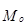> > 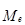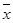, 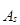< 0.
Степень асимметрии можно определить как отношение момента третьего порядка к среднему квадратическому отклонению в кубе по формуле =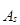 
.
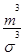Асимметрия выше 0,5 (без учета знака) считается значительной, меньше 0,25 – незначительной.
Для нормального распределения характерны следующие зависимости:
R =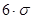 
и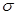 
= 
.
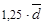Под эксцессом распределения понимается высоковершинность или низковершинност ь распределения по сравнению с нормальным распределением.
При высоковершинности наблюдается скопление частот в середине ряда, а при низковершинности – разбросанность частот ряда.
Для характеристики степени эксцесса применяется коэффициент эксцесса (Е)
Е =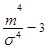 
,
где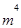 
– момент четвертого порядка
.
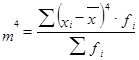Если Е = 0 – нормальное распределение;
Е > 0 – выше нормального;
Е < 0 – ниже нормального.
