2015-03-20
2122
Использование данного теста предполагает использование Q- статистики, значение которой определяется по формуле:
,
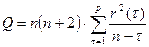где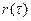 
- выборочные значения автокорреляционной функции;
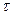- величина лага;
n – число наблюдений.
Q - статистика имеет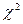 
- распределение с 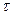степенями свободы. Если Q - статистика меньше табличного 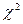, то гипотеза об отсутствии автокорреляции принимается.
Рассчитаем для нашей задачи Q – статистику. Для этого необходимо определить коэффициенты автокорреляции. Максимальная величина лага не должна превышать ¼ числа наблюдений, т.е. в рассматриваемом примере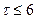 
. Следовательно нужно определить автокорреляции до шестого порядка. Для этого используем функцию Excel сервис – анализ данных – корреляция (рисунок 3.11).
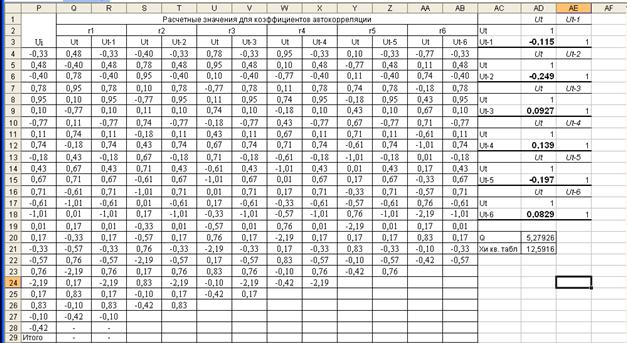
Рисунок 3.11 – Расчет Q-статистики Льюинга – Бокса
Подставив полученное значение в формулу, получим:
.
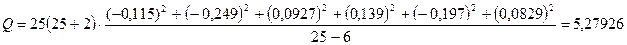Табличное значение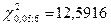 
.
Фактическое значение статистики меньше критического, следовательно, гипотеза принимается, т.е. в ряду остатков отсутствует автокорреляция.
