Тест ранговой корреляции Спирмена

Выдвигаются гипотезы:

Н_о: 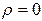(отсутствие гетероскедастичности);

Н₁: 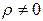(наличие гетероскедастичности).

Значения х_i и абсолютные величины u_i ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:

,

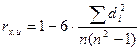где d_i - разность между рангами х_i и u_i, i = 1, 2,..., n;

n - число наблюдений.

Рассчитаем теоретические значения 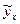по уравнению регрессии и найдем остатки. Ранжируем совокупность по возрастанию (рисунок 3.6).

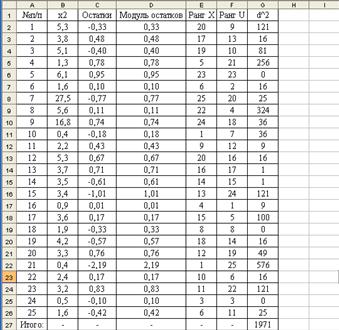
Рисунок 3.6 – Расчетная таблица для проведения теста Спирмена

Тогда .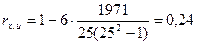

Если коэффициент корреляции 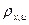для генеральной совокупности равен нулю, то статистика

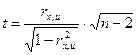
имеет распределение Стьюдента с числом степеней свободы v=n-2. Следовательно, если наблюдаемое значение t-статистики превышает табличное, то необходимо отклонить гипотезу о равенстве нулю коэффициента корреляции 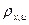, а следовательно, и об отсутствии гетероскедастичности.

В нашем примере статистика Стьюдента равна: .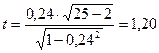

Табличное значение статистики Стьюдента составит t_{(0,05; 23)}=2,0687.

Таким образом, мы получили, что расчетное значение меньше табличного, следовательно, гипотеза об отсутствии гетероскедастичности принимается на уровне значимости 5 %.

Аналогично проводится анализ для фактора х₃.

Тест Уайта (White test).

Выдвигаются гипотезы:

Н_о: 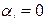- уравнение статистически незначимо (гомоскедастичность);

Н₁: 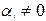- уравнение статистически значимо (гетероскедастичность).

Тест Уайта позволяет оценить количественно зависимость дисперсии ошибок регрессии 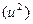от значений фактора x, используя квадратичную функцию:

,

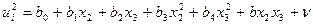где 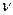- нормально распределенная ошибка.

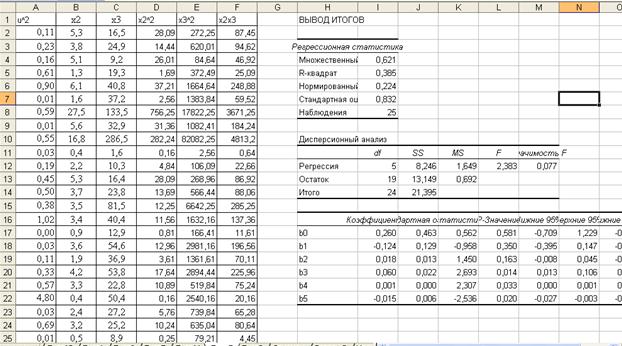
Рисунок 3.7 – Вывод итогов вспомогательной регрессии теста Уайта

Проводится этот тест следующим образом:

1) получаем регрессионные остатки u_i;

2) оцениваем вспомогательную регрессию;

Гипотеза об отсутствии гетероскедастичности принимается в случае незначимости регрессии в целом.

3) в нашем примере вспомогательная регрессия принимает вид:

.

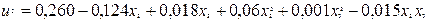Уравнение статистически незначимо на уровне значимости 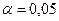. Следовательно, гипотеза об отсутствии гетероскедастичности принимается.

2 Если будет обнаружена гетероскедастичность остатков, примените для исходных данных ОМНК, предполагая, что .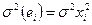

По всем проведенным тестам можно сделать вывод о гомоскедастичности регрессионных остатков. В противном случае для устранения гетероскедастичности необходимо применить к исходным данным обобщенный метод наименьших квадратов в предположении, что .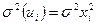

Исходное уравнение преобразуем делением правой и левой частей на x₂: 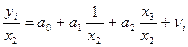. К нему применим МНК. Полученное уравнение имеет вид: 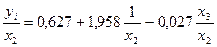(рисунок 3.8). Получены новые оценки параметров линейного уравнения, в котором смягчена гетероскедастичность.

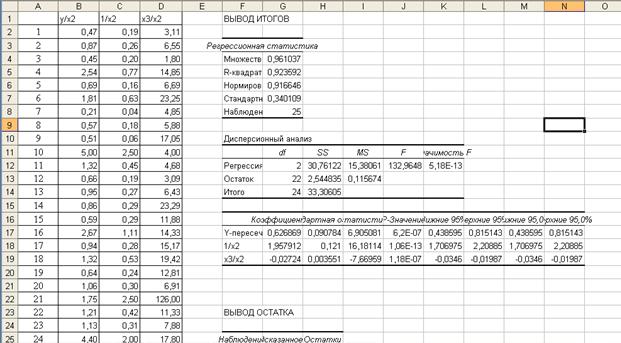
Рисунок 3.8– Вывод итога ОМНК

Проверить остатки на наличие автокорреляции первого порядка, используя метод рядов, критерий Дарбина – Уотсона и Q- статистику Льюинга – Бокса. Если гипотеза об отсутствии автокорреляции первого порядка не будет отвергнута, то применить ОМНК для оценивания параметров уравнения регрессии