Функция 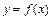 называется возрастающей (убывающей) на интервале
называется возрастающей (убывающей) на интервале 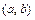 , если для любых
, если для любых 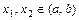 , удовлетворяющих условию
, удовлетворяющих условию 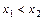 , выполняется неравенство
, выполняется неравенство 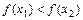 (
(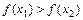 ).
).
Если функция 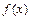 дифференцируема на интервале
дифференцируема на интервале 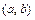 и
и 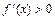 (
(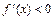 ) при всех
) при всех 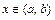 , то функция
, то функция 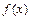 возрастает (убывает) на
возрастает (убывает) на 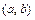 .
.
Точка 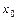 , принадлежащая области определения
, принадлежащая области определения 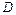 функции
функции 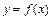 , называется критической точкой функции, если в этой точке
, называется критической точкой функции, если в этой точке 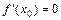 или
или 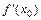 не существует. Критические точки функции
не существует. Критические точки функции 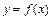 разбивают её область определения
разбивают её область определения 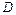 на интервалы монотонности (интервалы возрастания и убывания).
на интервалы монотонности (интервалы возрастания и убывания).
Точка 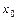 называется точкой минимума (максимума) функции
называется точкой минимума (максимума) функции 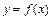 , если существует окрестность точки
, если существует окрестность точки 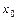 такая, что для всех точек
такая, что для всех точек 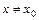 этой окрестности выполняется неравенство
этой окрестности выполняется неравенство  (
(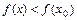 ), а число
), а число 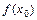 - минимумом (максимумом) функции. Точки минимума и максимума функции называются точками экстремума, а значения функции в этих точках – экстремумами функции.
- минимумом (максимумом) функции. Точки минимума и максимума функции называются точками экстремума, а значения функции в этих точках – экстремумами функции.
Необходимое условие экстремума. Если 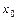 - точка экстремума функции
- точка экстремума функции 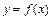 , то
, то 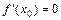 или
или 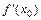 не существует.
не существует.
Первое достаточное условие экстремума. Пустьфункция 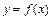 дифференцируема в окрестности точки
дифференцируема в окрестности точки 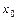 , в которой
, в которой 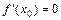 или
или 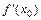 не существует. Тогда, если производная
не существует. Тогда, если производная 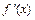 , при переходе слева направо через точку
, при переходе слева направо через точку 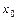 : 1) меняет знак с «+» на «
: 1) меняет знак с «+» на «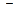 », то
», то 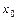 - точка максимума; 2) меняет знак с знак с «
- точка максимума; 2) меняет знак с знак с «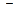 » на «+», то
» на «+», то 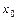 - точка минимума; 3) сохраняет знак, то
- точка минимума; 3) сохраняет знак, то 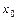 не является точкой экстремума.
не является точкой экстремума.
Второе достаточное условие экстремума. Пустьфункция 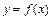 дважды дифференцируема в точке
дважды дифференцируема в точке 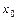 , в которой
, в которой 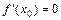 ,
, 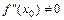 . Тогда: 1) если
. Тогда: 1) если 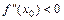 , то
, то 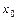 - точка максимума; 2) если
- точка максимума; 2) если 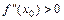 , то
, то 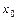 - точка минимума.
- точка минимума.
В задачах 5.221-5.234 для указанных функций найти интервалы возрастания и убывания:
5.221 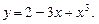 5.222
5.222 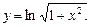
5.223 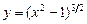 . 5.224
. 5.224 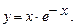
5.225 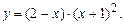 5.226
5.226 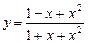 .
.
5.227 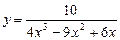 . 5.228
. 5.228 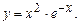
5.229 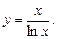 5.230
5.230 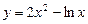 .
.
5.231 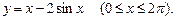 5.232
5.232 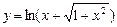 .
.
5.233 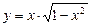 . 5.234
. 5.234 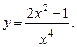
В задачах 5.235-5.248 для указанных функций найти экстремумы:
5.235 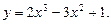 5.236
5.236 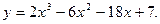
5.237 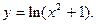 5.238
5.238 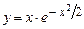 .
.
5.239 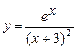 . 5.240
. 5.240 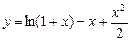 .
.
5.241 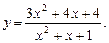 5.242
5.242 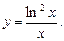
5.243 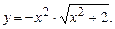 5.244
5.244 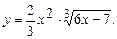
5.245 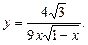 5.246
5.246 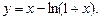
5.247 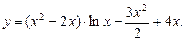
5.248 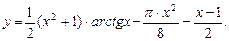
 2015-03-20
2015-03-20 1233
1233
