Теорема Ролля. Если функция 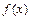 непрерывна на отрезке
непрерывна на отрезке 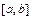 , дифференцируема на интервале
, дифференцируема на интервале 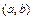 и
и 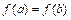 , то на
, то на 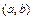 существует точка
существует точка 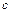 такая, что
такая, что 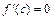 .
.
Теорема Лагранжа. Если функция 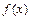 непрерывна на отрезке
непрерывна на отрезке 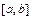 и дифференцируема на интервале
и дифференцируема на интервале 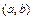 , то на
, то на 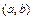 существует точка
существует точка 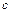 такая, что
такая, что 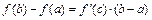 (формула Лагранжа).
(формула Лагранжа).
Теорема Коши. Если функции 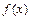 и
и 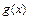 непрерывны на отрезке
непрерывны на отрезке 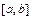 , дифференцируемы на интервале
, дифференцируемы на интервале 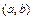 и
и 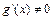 при всех
при всех 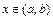 , то на интервале
, то на интервале 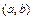 существует точка
существует точка 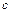 такая, что
такая, что
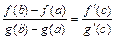 (формула Коши).
(формула Коши).
5.150 Проверить, выполняется ли теорема Ролля для следующих функций и, если выполняется, то для каких значений 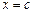 :
:
а) 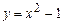 на отрезке
на отрезке 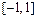 ; б)
; б) 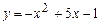 на отрезке
на отрезке 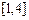 ; в)
; в) 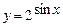 на отрезке [0,
на отрезке [0, 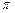 ]; г)
]; г) 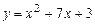 на отрезке
на отрезке 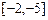 .
.
5.151 Функция 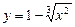 обращается в нуль при
обращается в нуль при 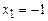 и
и 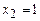 , но тем не менее
, но тем не менее 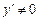 для всех
для всех 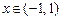 . Объяснить кажущееся противоречие с теоремой Ролля.
. Объяснить кажущееся противоречие с теоремой Ролля.
5.152 Проверить, выполняется ли теорема Лагранжа для следующих функций и, если выполняется, то для каких значений 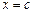 :
:
а) 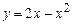 на отрезке [1, 3]; б)
на отрезке [1, 3]; б) 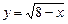 на отрезке
на отрезке 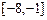 ; в)
; в) 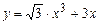 на отрезке [0,1]; г)
на отрезке [0,1]; г) 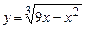 на отрезке
на отрезке 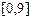 .
.
5.153 Объяснить почему не может быть применена теорема Лагранжа для функции 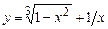 на отрезках:
на отрезках:
а) 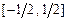 ; б)
; б) 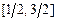 .
.
5.154 Проверить, выполняется ли теорема Коши для следующих функций и, если выполняется, то для каких значений 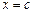 :
:
а) 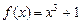 и
и 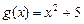 на отрезке
на отрезке 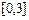 ;
;
б) 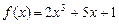 и
и 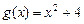 на отрезке
на отрезке 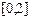 .
.
Если функция 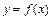 имеет производные всех порядков до
имеет производные всех порядков до 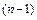 -го включительно в некоторой окрестности точки
-го включительно в некоторой окрестности точки 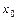 и кроме того имеет производную
и кроме того имеет производную 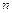 -го порядка
-го порядка 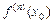 в самой точке
в самой точке 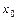 , то при
, то при 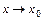 имеет место формула Тейлора (порядка
имеет место формула Тейлора (порядка 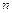 ) с остаточным членом в форме Пеано
) с остаточным членом в форме Пеано
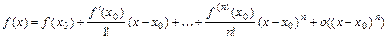 .
.
Если предположить существование 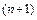 -ой производной
-ой производной 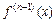 в окрестности точки
в окрестности точки 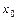 то для любой точки
то для любой точки 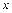 из этой окрестности имеет место формула Тейлора (порядка
из этой окрестности имеет место формула Тейлора (порядка 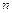 ) с остаточным членом в форме Лагранжа
) с остаточным членом в форме Лагранжа
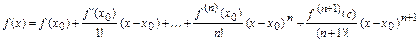 где
где 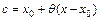 ,
, 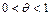 .
.
Формула Тейлора (с остаточным членом в любой форме) в частном случае 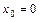 обычно называется формулой Маклорена.
обычно называется формулой Маклорена.
Формула Тейлора используется при вычислении значений функции с заданной степенью точности 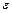 , при вычислении пределов функций.
, при вычислении пределов функций.
Из формулы Тейлора с остаточным членом в форме Лагранжаследует, что 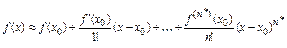 , где
, где 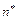 -минимальный из номеров
-минимальный из номеров 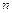 для которых
для которых 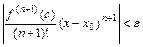 .
.
При вычислении пределов функций используют формулу Тейлора с остаточным членом в форме Пеано.
5.155 Разложить многочлен 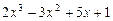 по степеням двучлена
по степеням двучлена 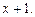
5.156 Разложить многочлен 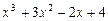 по степеням двучлена
по степеням двучлена 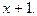
5.157 Разложить многочлен 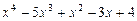 по степеням двучлена
по степеням двучлена 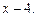
5.158 Разложить функцию 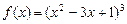 по степеням
по степеням 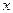 .
.
5.159 Для многочлена 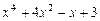 написать формулу Тейлора 2-го порядка в точке
написать формулу Тейлора 2-го порядка в точке 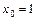 . Записать остаточный член в форме Лагранжа и найти значение
. Записать остаточный член в форме Лагранжа и найти значение 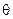 , соответствующее следующим значениям аргумента: а)
, соответствующее следующим значениям аргумента: а) 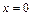 ; б)
; б) 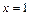 ; в)
; в) 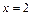 .
.
В задачах 5.160-5.164 написать формулы Маклорена 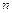 -го порядка (без остаточного члена) для следующих функций.
-го порядка (без остаточного члена) для следующих функций.
5.160 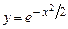 . 5.161
. 5.161 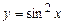 . 5.162
. 5.162 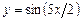 .
.
5.163 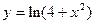 . 5.164
. 5.164 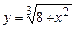 .
.
5.165 Написать разложения по степеням 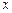 до членов указанного порядка включительно следующих функций:
до членов указанного порядка включительно следующих функций:
а) 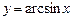 до члена с
до члена с 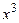 ; б)
; б) 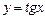 до члена с
до члена с 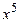 ;
;
в) 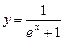 до члена с
до члена с 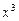 .
.
5.166. Написать разложения по степеням 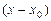 до членов указанного порядка включительно следующих функций:
до членов указанного порядка включительно следующих функций:
а) 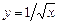 до члена с
до члена с 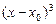 ;
; 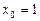 ;
;
б) 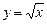 до члена с
до члена с 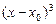 ;
; 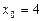 .
.
5.167. Оценить абсолютную погрешность приближённых формул: а) 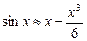 при
при 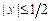 ; б)
; б) 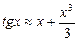 при
при 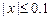 ;
;
в) 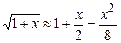 при
при 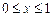 .
.
В задачах 5.168-5.169 используя разложения функций по формуле Маклорена вычислить следующие пределы:
5.168 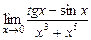 . 5.169.
. 5.169. 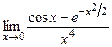 .
.
5.170 Вычислить с абсолютной погрешностью, не превосходящей 0.001, приближенные значения следующих чисел:
а) sin 1; б) 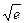 ; в)
; в) 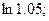 г).
г). 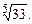
 2015-03-20
2015-03-20 762
762








