Дифференциал. Если функция дифференцируема в точке , то её приращение может быть представлено в виде

Если функция 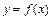дифференцируема в точке 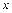, то её приращение 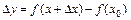может быть представлено в ви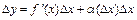де:

, где 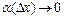при .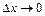

Дифференциалом 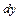функции 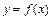в точке 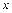называется главная, линейная относительно 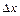часть 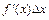приращения 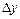функции: 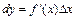. В частности, для функции 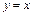имеем 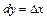, т.е. дифференциал независимого переменного 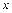совпадает с приращением 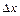. Поэтому дифференциал функции 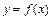записывается в виде 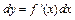. Форма записи первого дифференциала не изменится и в том случае, если переменная 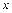является функцией от новой независимой переменной (свойство инвариантности формы первого дифференциала).

Для функции одной переменной 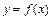существование в точке 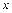её дифференциала 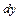и производной 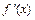равносильны.

Дифференциалом 2-ого порядка функции 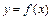называется дифференциал от её первого дифференциала и обозначается 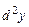, т. е. 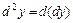. В общем дифференциалом порядка 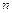называется дифференциал от дифференциала 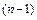-ого порядка и обозначается 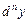, т.е. .

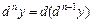Если 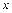- независимая переменная, то для нахождения дифференциала 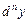функции 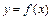справедлива формула .

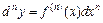Первый дифференциал применяют для приближённого вычисления значений функции 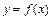в малой окрестности точки 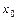, в которой функция дифференцируема, по формуле:

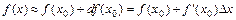, где .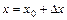

Чем меньше значение 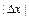, тем точнее приближённая формула.

5.97 Найти приращение 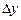и дифференциал 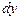функции 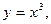соответствующие значению аргумента 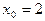и двум различным приращениям аргумента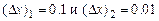

5.98 Какое приращение получает функция 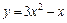при переходе независимой переменной от значения 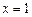к значению 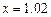. Каково значение соответствующей линейной главной части? Найти отношение второй величины к первой.

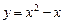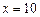5.99 Найти приращение и дифференциал функции при и 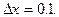Вычислить абсолютную 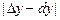и относительную 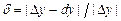погрешности, которые получаются при замене приращения дифференциалом.

5.100 Найти приращение 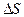и дифференциал 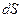площади S квадрата, соответствующие приращению 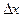стороны x.

5.101 Найти приращение 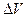объема V шара при изменении радиуса R =2 на 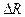. Вычислить 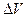, если 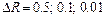. Какова будет погрешность значения 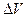, если ограничиться членом, содержащим 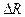в первой степени?

В задачах 5.102-5.113 найти дифференциалы функций:

5.102 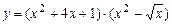. 5.103 .

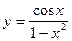5.104 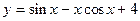. 5.105 .

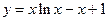5.106 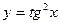. 5.107 .

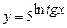5.108 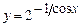. 5.109 .

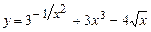5.110 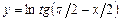. 5.111 .

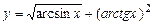5.112 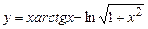. 5.113 .

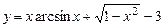В задачах 5.114-5.118 найти дифференциалы второго порядка следующих функций:

5.114 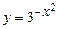. 5.115 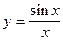. 5.116 .

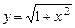5.117 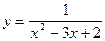. 5.118 .

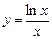5.119 Найти приближенное значение функци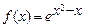и при .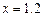

5.120 Найти приближенное значение функци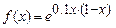и при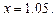

В задачах 5.121-5.126 вычислить приближенно:

5.121 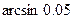. 5.122 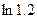. 5.123 .

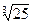5.124 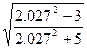. 5.125 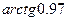. 5.126 .

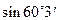§3. Некоторые приложения производной.

3.1. Геометрические приложения производной.

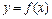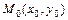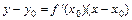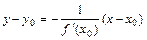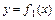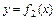Уравнение касательной к графику функции в точке имеет вид: , а уравнение нормали - вид: . Углом между двумя кривыми и в точке их пересечения 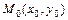называется угол 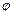между касательными к этим кривым в точке 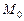, тангенс которого вычисляется по формуле: .

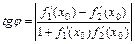В задачах 5.127-5.130 составить уравнения касательной и нормали к данным линиям в указанных точках.

5.127 а) ;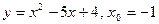

б) , 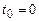; в) , .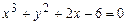

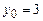5.128 а) ;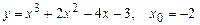

б) , ;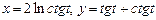

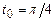в) .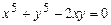

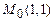5.129 а) 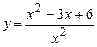, 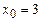; б) , , ;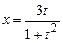

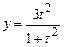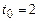в) , .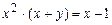

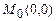5.130 а) 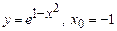; б) , , ;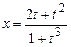

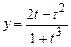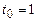в) , .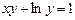

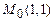5.131. Найти углы, под которыми пересекаются данные линии:

а) 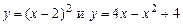; б)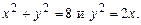

5.132 Составить уравнения касательных к линии 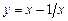в точках ее пересечения с осью абсцисс.

5.133 В какой точке 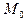кривой 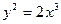касательная перпендикулярна к прямой ?

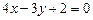5.134 Найти коэффициенты 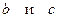в уравнении параболы 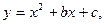касающейся прямой 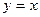в точке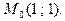

5.135 Показать, что касательные к гиперболе 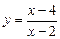в точках её пересечения с осями координат параллельны между собой.

5.136 Составить уравнение нормали к графику функции 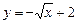в точке её пересечения с биссектрисой первого координатного угла.

5.137 Составить уравнение нормали к параболе 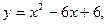которая перпендикулярна к прямой, соединяющей начало координат с вершиной параболы.

5.138 На линии 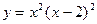найти точки, в которых касательные к ней параллельны оси абсцисс.

5.139 В каких точках линии 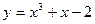касательная к ней параллельна прямой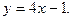

5.140 Составить уравнение касательной к линии 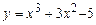перпендикулярной к прямой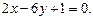

3.2 Механические приложения производной.

Если 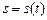-функция, описывающая закон движения материальной точки, то первая производная 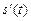есть скорость, а вторая производная 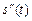- ускорение этой точки в момент времени 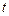(механический смысл первой и второй производных).

5.141 Точка движется прямолинейно по закону 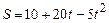Найти скорость 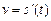и ускорение 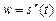движения. Чему равны скорость и ускорение в момент времени ?

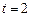5.142 Точка движется по прямой так, что ее расстояние S от начального пункта через время t равно .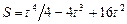

а) В какие моменты точка была в начальном пункте?

б) В какие моменты ее скорость равна нулю?

5.143 Тело массой 3кг движется прямолинейно по закону 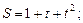S- выражено в сантиметрах, t - в секундах. Определить кинетическую энергию 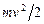тела через 5 секунд после начала движения в Дж ().

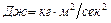5.144 Угол 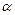поворота шкива в зависимости от времени t задан функцией 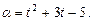Найти угловую скорость 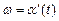в момент времени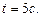

5.145 Колесо вращается так, что угол поворота пропорционален квадрату времени. Первый оборот был сделан колесом за 8с. Найти угловую скорость 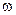через 32с после начала движения.