Случайный вектор 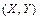 называется (абсолютно) непрерывным, если его функция распределения представляется в виде
называется (абсолютно) непрерывным, если его функция распределения представляется в виде 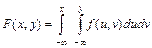 ,
, 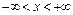 ,
, 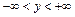 , где
, где 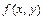 -неотрицательная и интегрируемая в бесконечных пределах функция, называемая функцией плотности вероятностей (совместной). Функция распределения
-неотрицательная и интегрируемая в бесконечных пределах функция, называемая функцией плотности вероятностей (совместной). Функция распределения 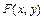 непрерывного случайного вектора
непрерывного случайного вектора 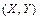 является непрерывной функцией на всей числовой плоскости.
является непрерывной функцией на всей числовой плоскости.
Функция 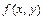 является плотностью вероятностей некоторого непрерывного случайного вектора
является плотностью вероятностей некоторого непрерывного случайного вектора 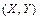 , тогда и только тогда, когда:
, тогда и только тогда, когда:
1) 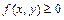 ; 2)
; 2) 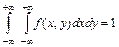 .
.
В точках непрерывности функции 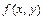 :
: 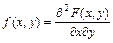 .
.
Для непрерывного случайного вектора 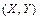 с плотностью вероятностей
с плотностью вероятностей 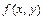 вероятность любого события вида
вероятность любого события вида 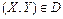 ,
, 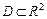 вычисляется по формуле:
вычисляется по формуле: 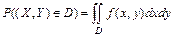 .
.
Частные плотности вероятностей компонент находятся интегрированием совместной плотности: 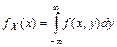 ,
, 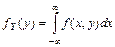 .
.
Непрерывные случайные величины 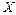 и
и 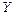 независимы тогда и только тогда, когда
независимы тогда и только тогда, когда 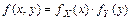 ,
, 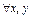 . В противном случае они зависимы.
. В противном случае они зависимы.
Числовые характеристики 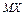 ,
, 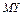 вычисляют по формулам:
вычисляют по формулам: 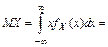
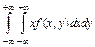 ,
, 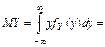
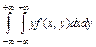
Вероятность события  , где
, где 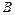 -постоянная величина, находится по формуле
-постоянная величина, находится по формуле 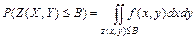 , где интегрирование распространяется на все значения переменных
, где интегрирование распространяется на все значения переменных 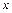 ,
, 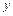 для которых
для которых 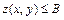 .
.
В задачах 12.221-12.222 двумерная непрерывная случайная величина 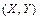 задана совместной функцией распределения
задана совместной функцией распределения 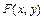 . Требуется: а) найти функции распределения составляющих случайных величин
. Требуется: а) найти функции распределения составляющих случайных величин 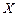 ,
, 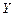 и выяснить являются они зависимыми или нет; б) найти совместную функцию плотности вероятностей
и выяснить являются они зависимыми или нет; б) найти совместную функцию плотности вероятностей 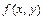 ; в) вычислить вероятность
; в) вычислить вероятность 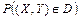 для указанной области
для указанной области 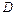 .
.
12.221 
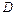 - прямоугольник
- прямоугольник 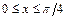 ,
, 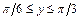 .
.
12.222 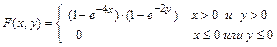
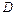 - квадрат
- квадрат 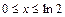 ,
, 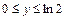 .
.
В задачах 12.223-12.224 двумерная случайная величина 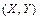 задана совместной функцией плотности вероятностей
задана совместной функцией плотности вероятностей 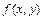 .Требуется:
.Требуется:
а) найти неизвестную постоянную 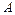 ; б) найти функции плотности вероятностей составляющих случайных величин
; б) найти функции плотности вероятностей составляющих случайных величин 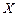 ,
, 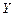 и выяснить являются они зависимыми или нет; в) вычислить
и выяснить являются они зависимыми или нет; в) вычислить 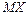 ,
, 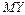 , а также вероятность
, а также вероятность 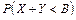 для указанного значения постоянной
для указанного значения постоянной 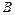 .
.
12.223 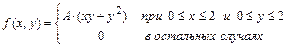
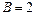 .
.
12.224 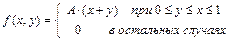
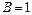 .
.
12.225 Двумерная случайная величина 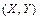 равномерно распределена в указанной области
равномерно распределена в указанной области 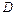 . Найти: совместную функцию плотности вероятностей
. Найти: совместную функцию плотности вероятностей 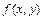 ; функции плотности вероятностей составляющих случайных величин
; функции плотности вероятностей составляющих случайных величин 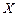 ,
, 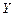 и выяснить являются они зависимыми или нет; центр рассеивания
и выяснить являются они зависимыми или нет; центр рассеивания 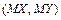 , если: а)
, если: а) 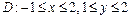 ;
;
б) 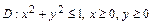 ; в)
; в) 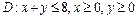 .
.
 2015-03-20
2015-03-20 742
742








