Для более детального описания функций, рекомендуем пользоваться системой помощи пакета MATLAB. Для вызова справки в командном окне пакета наберите: >>help имя функции.
Таблица 1. Описание математических операций
| Операция | Описание |
| a+b | сложение |
| a-b | вычитание |
| a=b | оператор присваивания |
| a.*b | поэлементное умножение |
| a*b | матричное умножение |
| a./b | правое поэлементное деление |
| a.\b | левое поэлементное деление |
| a/b | правое матричное деление |
| a\b | левое матричное деление |
| a.^b | поэлементное возведение в степень |
| a^b | матричное возведение в степень |
| a<b | меньше |
| a>b | больше |
| a<=b | меньше или равно |
| a>=b | больше или равно |
| a~=b | неравно |
| a==b | равно |
| a&b | логическое И |
| a|b | логическое ИЛИ |
| ~a | логическое НЕ |
| a.’ | транспонирование |
| a’ | комплексно-сопряженное транспонирование |
| [a b] | горизонтальная конкатенация |
| [a;b] | вертикальная конкатенация |
| a(s1,s2,…,sn) | ссылка по индексу |
| a(s1,s2,…,sn)=b | присваивание по индексу |
| b(a) | индексирование |
Таблица 2. Обозначения системных переменных MATLAB
| Переменная | Значение переменной |
| i,j | мнимая единица ( 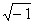 ) ) |
| pi | число 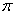 (3.14159265) (3.14159265) |
| eps | погрешность для операций над числами с плавающей точкой (по умолчанию 2-52) |
| realmin | минимальное значение вещественного числа (2-1022) |
| realmax | максимальное значение вещественного числа (2-1023) |
| inf | бесконечность ( 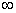 ) ) |
| naN | неопределенность (например, 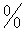 ) ) |
| ans | переменная, хранящая результат последней операции |
Таблица 3. Функции комплексных переменных
| Функция | Описание |
| abs | абсолютное значение комплексного числа |
| conj | комплексно-сопряженное число |
| imag | мнимая часть комплексного числа |
| real | действительная часть комплексного числа |
| angle | аргумент комплексного числа |
| isreal | "истина", если число действительное |
Таблица 4. Стандартные функции вещественного аргумента
| Обозначение | Описание | |||
| Экспоненциальные функции | ||||
| а^х | степенная функция | |||
| х^а | показательная функция | |||
| sqrt(x) | квадратный корень | |||
| ехр(х) | экспонента | |||
| log(x) | натуральный логарифм | |||
| log10(x) | десятичный логарифм | |||
| abs(x) | модуль | |||
| fix(x) | отбрасывание дробной части числа | |||
| floor(x) | округление до меньшего целого | |||
| ceil(x) | округление до большего целого | |||
| round(x) | обычное округление | |||
| rem(x,y) | остаток от деления x на y без учета знака | |||
| mod(x,y) | остаток от деления x на y с учетом знака | |||
| sign(x) | знак числа | |||
| factor(x) | разложение числа x на простые множители | |||
| Функциипреобразования координат | ||||
| Cart2sph | преобразование декартовых координат в сферические | |||
| cart2pol | преобразование декартовых координат в полярные | |||
| pol2cart | преобразование полярных координат в декартовы | |||
| Другие функции | ||||
| gсd(a,b) | наибольший общий делитель | |||
| lcm(a,b) | наименьшее общее кратное | |||
| legendre(n,x) | обобщенная функция Лежандра | |||
| log2(x) | логарифм по основанию 2 | |||
| pow2(n) | возведение числа 2 в степень n | |||
| rat(x) | представление числа в виде рациональной дроби | |||
| primes(n) | формирование списка простых чисел | |||
| Тригонометрические функции | ||||
| sin(x) | синус | |||
| sinh(x) | синус гиперболический | |||
| asin(x) | арксинус | |||
| asinh(x) | арксинус гиперболический | |||
| cos(x) | косинус | |||
| cosh(x) | косинус гиперболический | |||
| acos(x) | арккосинус | |||
| acosh(x) | арккосинус гиперболический | |||
| tan(x) | тангенс | |||
| tanh(x) | тангенс гиперболический | |||
| atan(x) | арктангенс | |||
| atanh(x) | арктангенс гиперболический | |||
| cot(x) | котангенс | |||
| coth(x) | котангенс гиперболический | |||
| acot(x) | арккотангенс | |||
| acoth(x) | арккотангенс гиперболический | |||
| sec(x) | секанс | |||
| asec(x) | арксеканс | |||
| asech(x) | арксеканс гиперболический | |||
| csc(x) | косеканс | |||
| csch(x) | косеканс гиперболический | |||
| acsc(x) | арккосеканс | |||
| acsch(x) | арккосеканс гиперболический | |||
| Функции комбинаторики | ||||
| perms(v) | вычисляет число перестановок | |||
| nchoose(n,k) | вычисляет количество сочетаний из n пo k | |||
 2015-03-20
2015-03-20 1186
1186








