Любое сооружение под действием внешних факторов деформируется, изменяя свою первоначальную форму и принимает форму равновесия, при котором влияние внешних воздействий уравновешивается внутренними силами сопротивления. При этом перемещение ∆ kP произвольной точки T по заданному направлению k – k от нагрузки Р может быть вычислено по универсальной формуле Мора, которая для балок и рам имеет вид:
∆ kP = 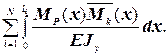
Вычисление интеграла Мора удобно производить по правилу Верещагина или правилу «перемножения» эпюр. Определение перемещений с помощь этого правила производится в следующем порядке:
1. Строится эпюра изгибающих моментов от действия заданной нагрузки - эпюра МР (грузовая эпюра);
2. Выбирается вспомогательное единичное состояние системы. Для этого к балке или раме, освобожденной от заданной нагрузки, по направлению искомого перемещения прикладывается единичная сила: при определении линейного перемещения – сосредоточенная сила, при определении угла поворота – сосредоточенный момент;
3. Строится эпюра изгибающих моментов от действия этой единичной силы –эпюра 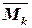 ;
;
4. Ось балки (рамы) разбивается на участки таким образом, чтобы в пределах участка эпюры МР и 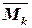 не имели бы особенностей (переломов и скачков);
не имели бы особенностей (переломов и скачков);
5. На каждом участке балки (рамы) для вычисления интеграла Мора по правилу Верещагина или правилу «перемножения» эпюр необходимо площадь одной эпюры (если есть криволинейная эпюра, то обязательно ее площадь) умножить на ординату другой эпюры, расположенную под центром тяжести первой, т.е.
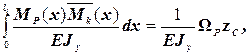
где 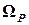 – площадь эпюры МР; z C – ордината в линейной эпюре
– площадь эпюры МР; z C – ордината в линейной эпюре 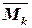 , под центром тяжести эпюры МР (рис.17); EJy –жесткость поперечного сечения балки (рамы).
, под центром тяжести эпюры МР (рис.17); EJy –жесткость поперечного сечения балки (рамы).
Результат «перемножения» эпюр является положительным, если эпюры МР и 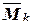 одного знака и – отрицательным, если эпюры МР и
одного знака и – отрицательным, если эпюры МР и 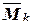 разных знаков.
разных знаков.
Если ∆ kP положительно, то перемещение совпадает с направлением единичной силы, а если отрицательно – то противоположно этому направлению.
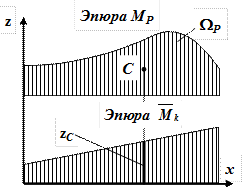 |
| Рис.17. Правило Верещагина |
На первый взгляд, описанный графоаналитический способ вычисления интегралов Мора не даёт упрощений, т.к. всё равно приходится вычислять площадь 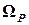 криволинейных эпюр. Однако встречающиеся на практике эпюры могут быть разбиты на ряд простых фигур (прямоугольник, треугольник, симметричную квадратичную параболу), у которых известны площадь и положение центра тяжести. Примеры разбиения эпюр приведены на рис. 18.
криволинейных эпюр. Однако встречающиеся на практике эпюры могут быть разбиты на ряд простых фигур (прямоугольник, треугольник, симметричную квадратичную параболу), у которых известны площадь и положение центра тяжести. Примеры разбиения эпюр приведены на рис. 18.
Рис. 18. Разбиение сложных эпюр на простые эпюры
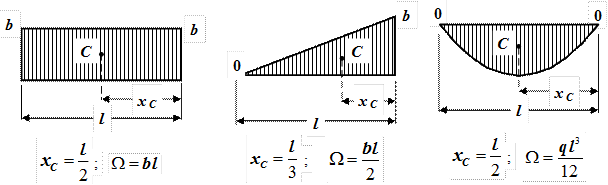 На рис.19 приведены сведения о координатах центра тяжести и площадях простейших эпюр – прямоугольник, треугольники и симметричная квадратичная парабола.
На рис.19 приведены сведения о координатах центра тяжести и площадях простейших эпюр – прямоугольник, треугольники и симметричная квадратичная парабола.
Рис. 19. Площади эпюр и их координаты центров тяжести
Пример. Определить прогиб (вертикальное перемещение) и угол поворота в сечения B в статически определимой балке (рис.20).
 |
Рис.20. Эпюры MP, 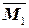 и и 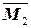 |
Решение.
 Значения изгибающих моментов.
Значения изгибающих моментов.
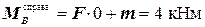 ;
; 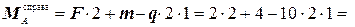
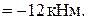
Строим эпюру МР от заданной нагрузки –это парабола, выпуклая вниз (рис.20 б).
Выбираем единичное состояние – освободив балку от заданной нагрузки, прикладываем в точке B сосредоточенную силу 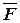 =1, направленную вертикально вниз. Строим эпюру
=1, направленную вертикально вниз. Строим эпюру 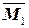 от единичного воздействия (рис.20 в).
от единичного воздействия (рис.20 в).
Эпюру от заданной нагрузки МР разбиваем на три простейшие (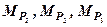 ) – два треугольника и симметричную параболу (рис.21).
) – два треугольника и симметричную параболу (рис.21).
Площади этих эпюр: 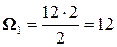 ;
; 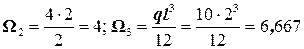 .
.
Ординаты в эпюре 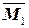 под центрами тяжести соответственно равны
под центрами тяжести соответственно равны 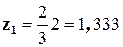 ;
; 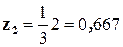 ;
; 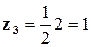 .
.
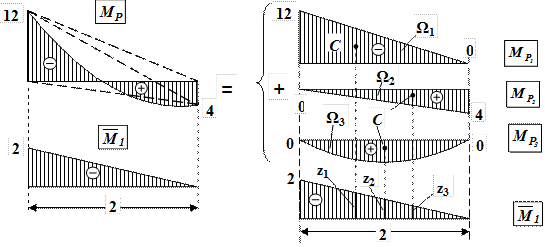
Рис.21. Разбиение сложной эпюры на простые эпюры. Перемножение эпюр
Прогиб в сечении B равен
v B =∆ 1P = 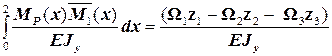 =
=
= 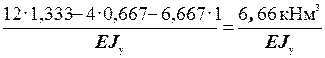 .
.
Положительное значение прогиба показывает, что точка B перемещается вниз в направлении единичной силы.
Для определения угла поворота выбираем единичное состояние – освободив балку от заданной нагрузки, прикладываем в точке B сосредоточенный момент 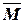 =1, направленный по ходу часовой стрелки. Строим эпюру
=1, направленный по ходу часовой стрелки. Строим эпюру 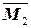 от единичного воздействия (рис.20 г). Поскольку ординаты эпюры от единичного момента везде равны единице, а площади простейших грузовых эпюр найдены выше, определяем угол поворота в сечении B
от единичного воздействия (рис.20 г). Поскольку ординаты эпюры от единичного момента везде равны единице, а площади простейших грузовых эпюр найдены выше, определяем угол поворота в сечении B
j B =∆ 2P = 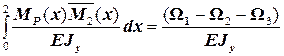 =
= 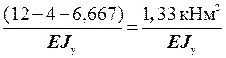 .
.
Положительное значение угла поворота показывает, что сечение B поворачивается по ходу часовой стрелки по направлению единичного момента.
 2015-03-20
2015-03-20 12396
12396
