2015-03-20
274
Уравнения, описывающие зависимость координат объекта и всех элементов системы от входных воздействий, а также структурная схема системы, составляют математическую модель системы.
Уравнения могут быть алгебраическими, трансцендентными, дифференциальными, интегральными, конечно-разностными и т.д. В общем случае уравнение можно записать в виде:
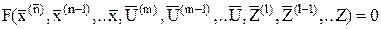
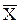или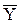 
- вектор координат объекта
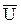- управляющее воздействие;
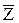- возмущающее воздействие.
Данное уравнение, связывающее координаты объекта, а также их производные и воздействия называют уравнением динамики.
Если все производные равны нулю, то уравнение превращается в уравнение статики (описывают либо безынерционные объекты, либо инерционные в установившемся состоянии при постоянных входных воздействиях)
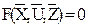
Уравнение статики связывает только текущие координаты и воздействия.
Если функция F линейная, то и система называется линейной.
Анализ и синтез линейных систем значительно проще нелинейных, но большинство объектов являются нелинейными, для них функция F- нелинейная. В ряде случаев при малых изменениях входных воздействий координат функцию F можно линеаризовать и объект рассматривать как линейный.
Системы могут быть одномерными (элементы системы зависят от одного воздействия и имеют одну выходную координату) и многомерными или многосвязными (элементы таких систем имеют несколько выходных координат, зависящих от нескольких входных воздействий).
Если коэффициенты в уравнениях постоянны во времени – объекты и системы – стационарные, если коэффициенты изменяются со временем – элементы и системы нестационарные.
В теории управления при анализе и синтезе систем управления их условно разделяют на отдельные участки – звенья.
Звено представляет собой отдельный участок, узел, блок и т.д., физически выделяемый или не выделяемый из системы, который выполняет определенную функцию и описывается простейшим уравнением.
Звенья также могут быть как безинерционными (усилительное или пропорциональное, дифференциальное) так и инерционными.
Обычно звено имеет один вход и один выход.
 |
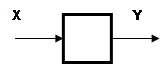В общем случае, для линейных звеньев уравнения, связывающие вход с выходом (уравнения состояния), можно записать как:
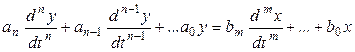
Если использовать оператор дифференцирования
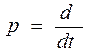
то уравнение можно записать в операторной форме:
(anpn+an-1pn-1+…a0p0) y(t)=(bmpm+…b0)x(t),
причем, умножение функции на pi имеет смысл дифференцирования этой функции i раз, p0=1; n – определяет порядок ДУ; An(p)= anpn+an-1pn-1+…a0p0, Bm(p)= =bmpm+…b0- многочлены (полиномы) n-ой и m- ой степени от p.
В более компактной форме дифференциальное уравнение имеет вид:
An(p)y(t)= Bm(p)x(t).
