Краткие сведения о преобразованиях Лапласа

Для функции f(t), дифференцируемой на интервале времени от 0 до ∞ и ограниченной по модулю (|f(t)|≤Me^-ct), изображением по Лапласу является функция F(s) полученная как:

где M, c – конечное значение, s - комплексная переменная Лапласа s=σ+jω

1. Преобразование Лапласа является линейной операцией.

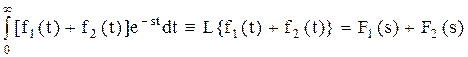
Преобразование Лапласа от суммы оригиналов равно сумме изображений.

L{Cf(t)}=CF(s), С=const.

2. Обратное преобразование.

,

,

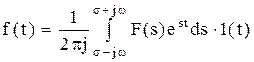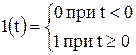т.е функция f(t) лежит в положительной области времени.

4. , ,

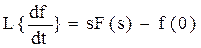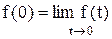L{f⁽ⁿ⁾ (t)}=sⁿF(s)-s^n-1f(0)-s^n-2f`-…..-f^n-1(0)

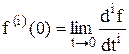
5.

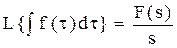
6. Правило предельного перехода.

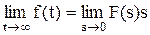
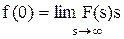
7.

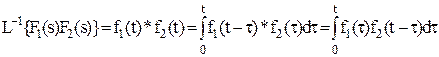
-интеграл свертки.

Верхний предел может быть равен ∞, нижний -∞, т.к функции f₁ и f₂ для отрицательного аргумента должны быть равны нулю.

8. Смещение оригинала, т.е.

L{f(t-τ)}=F(s)e^-sτ

9. Теорема о разложении, или теорема о вычетах:

если 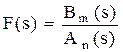дробно-рациональная функция, причем, m<n, то

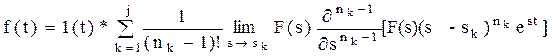
где, j- количество различных корней; n_k-число повторений к-го корня;

s_k- корни уравнения A_n(s)=0.