Можно показать, что справедливо соотношение, называемое первым замечательным пределом:
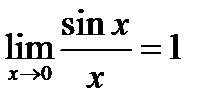 .
.
Рассмотрим на примере, как можно использовать данную формулу для разрешения особенностей тригонометрических функций в конечных точках.
Задача 2.1.в. Вычислить
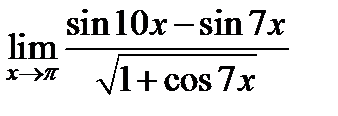 .
.
Решение. Убедимся, что мы имеем дело с неопределенностью вида 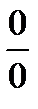 . При
. При 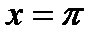 получаем:
получаем:
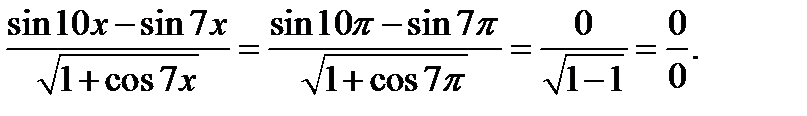
Прежде всего, сделаем замену переменной 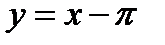 , так, чтобы новая переменная
, так, чтобы новая переменная 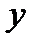 стремилась к 0, когда
стремилась к 0, когда 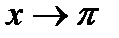 :
:
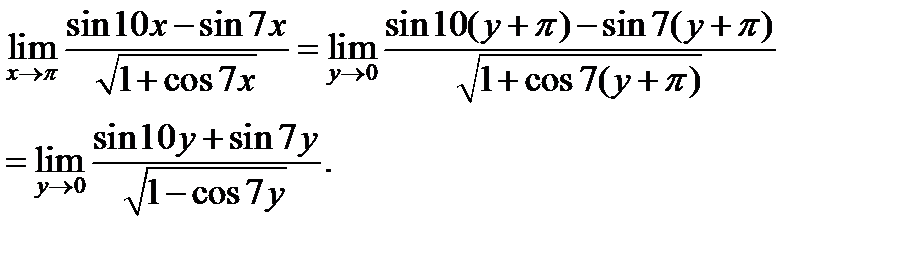
Используя формулу преобразования суммы синусов в произведение и формулу для косинуса двойного угла, получаем
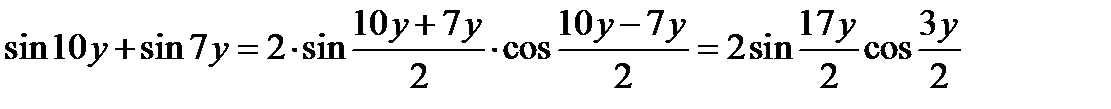
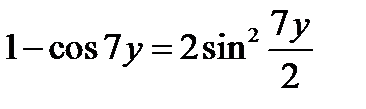 .
.
Отсюда
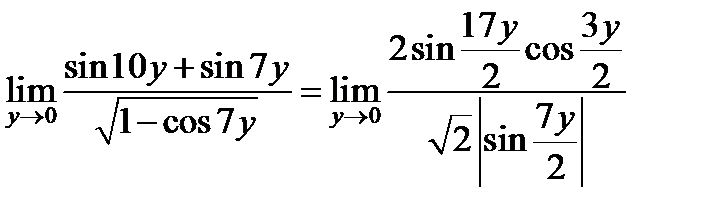 .
.
Пусть сначала 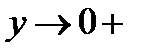 , тогда
, тогда 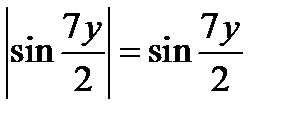 . Чтобы свести полученное выражение к формуле
. Чтобы свести полученное выражение к формуле 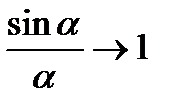 , поделим и умножим
, поделим и умножим 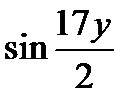 на
на 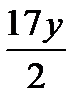 , а
, а 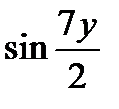 на
на 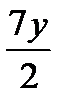 :
:
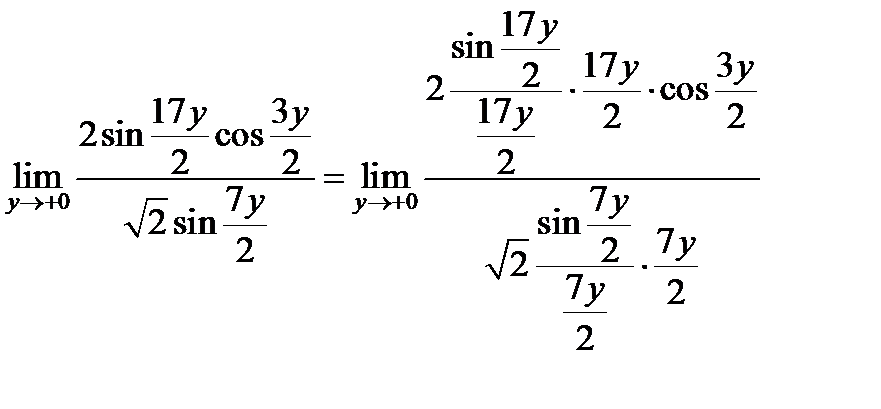
Заменяя пределы дробей 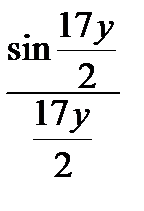 и
и 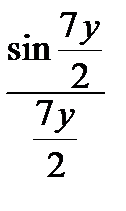 на 1, получаем
на 1, получаем
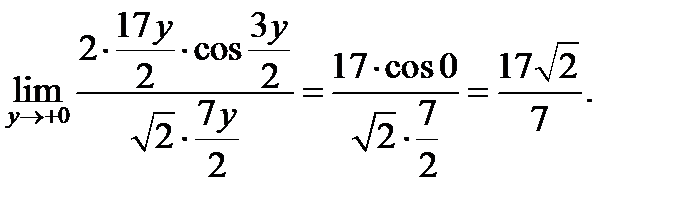
При 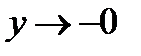 имеем
имеем 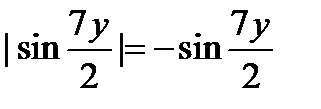 , и предел отличается только знаком:
, и предел отличается только знаком:
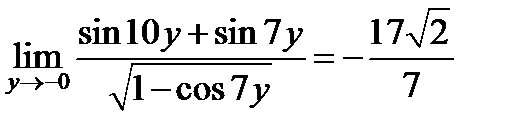 .
.
 2015-03-20
2015-03-20 356
356








