Производной функции 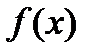 в точке
в точке 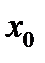 называется предел
называется предел
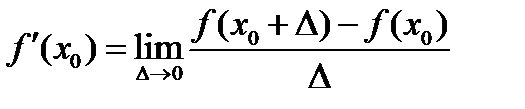 .
.
Наряду с обозначением 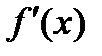 для производной используется еще обозначение
для производной используется еще обозначение 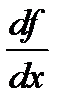 .
.
Производные основных элементарных функций приведены в следующей таблице.
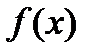
| 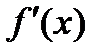
|
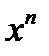
| 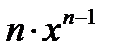
|
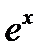
| 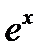
|
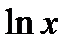
| 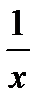
|
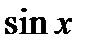
| 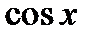
|
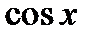
| 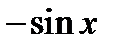
|
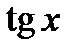
| 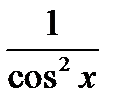
|
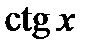
| 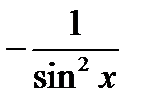
|
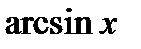
| 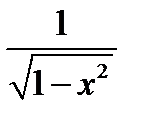
|
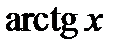
| 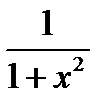
|
Рассмотрим дифференцирование степенной функции при некоторых 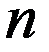 .
.
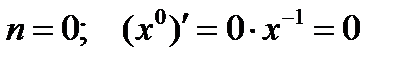
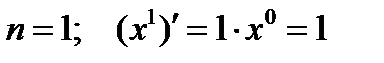
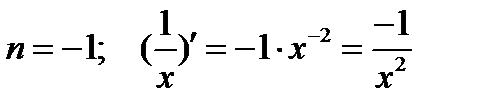
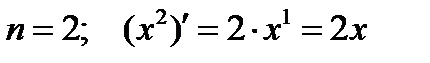
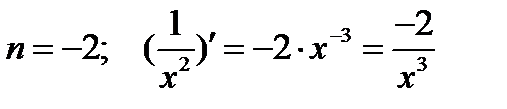
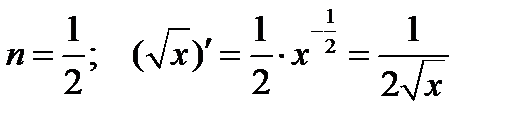
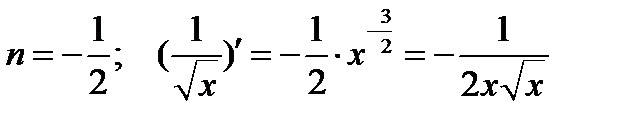
Имеется два основных приема дифференцирования функций
1) Формуладифференцирования произведения и частного двух функций
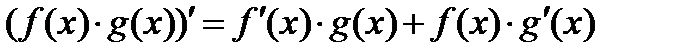 ,
,
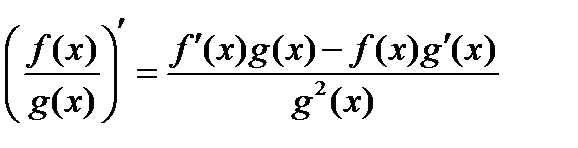 .
.
2) Формула дифференцирования композиции (или сложной функции)
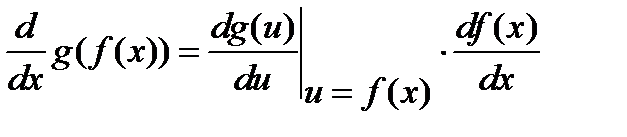 .
.
Примеры дифференцирования сложной функции.
1°) 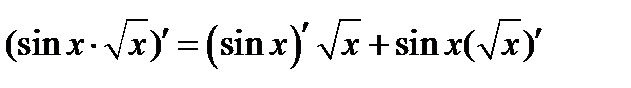
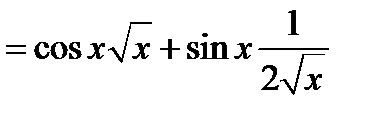
2°) 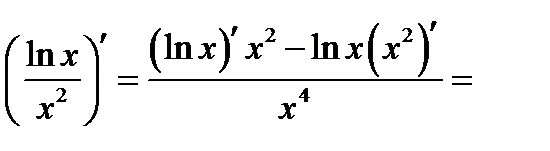
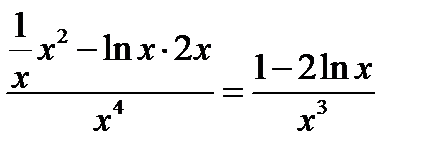
3°) 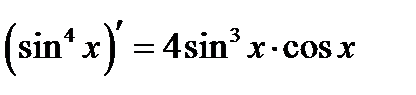
4°) 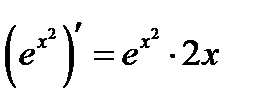
5°) 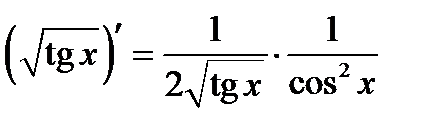
6°) 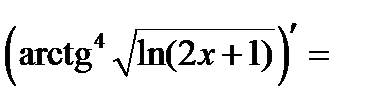
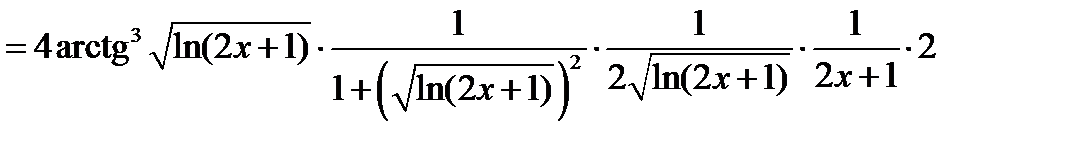
В задачах 2.2.а-2.2.з для функции 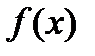 требуется найти производную
требуется найти производную 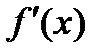 .
.
Задача 2.2.а 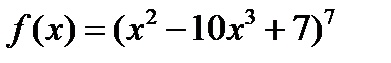 .
.
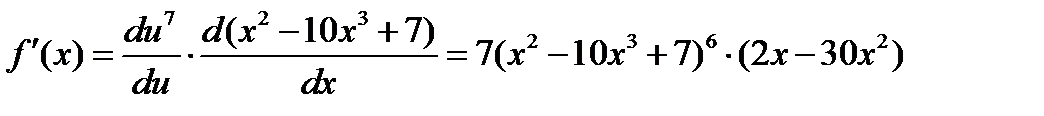 .
.
Задача 2.2.б 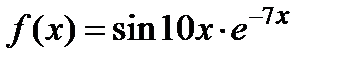 .
.
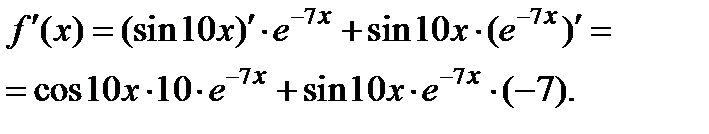
Задача 2.2.в 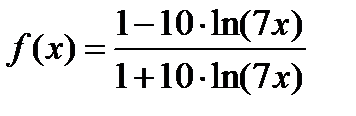 .
.
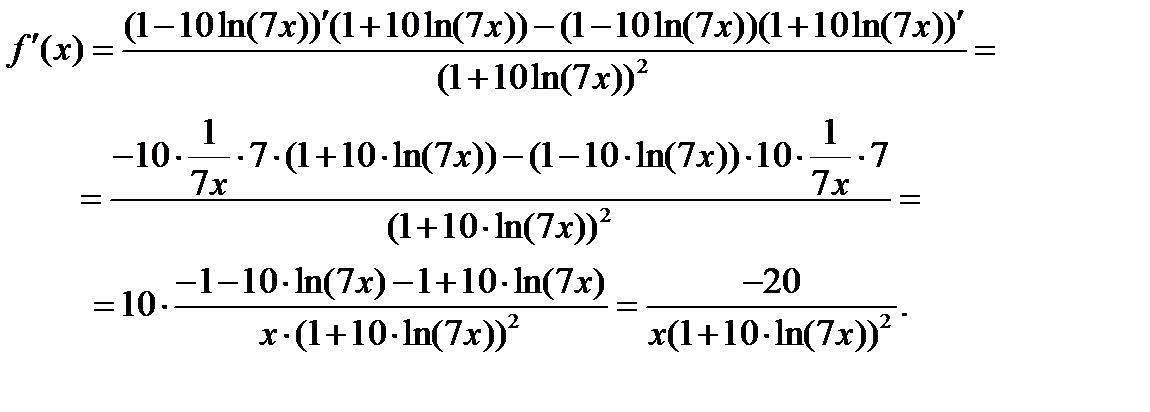 Задача 2.2.г
Задача 2.2.г 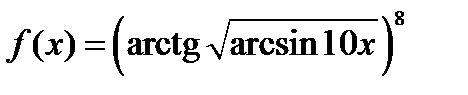 .
.
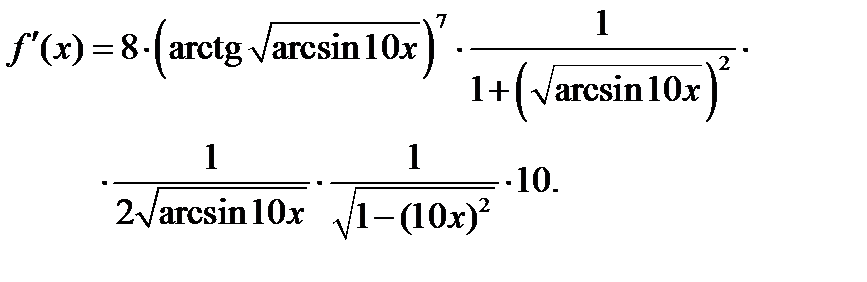
 2015-03-20
2015-03-20 214
214







