Предел и производная.
Начнем с определения Вейерштрасса предела функции в конечной точке и на бесконечности.
Определение 1. Число 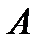 называется пределом функции
называется пределом функции 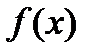 в точке
в точке 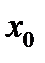 , если для любого
, если для любого 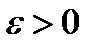 найдется такое положительное число
найдется такое положительное число 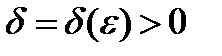 , что для любого
, что для любого 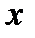 , удовлетворяющего неравенству
, удовлетворяющего неравенству 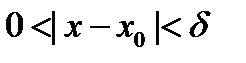 , справедлива оценка
, справедлива оценка 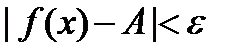 . В этом случае пишут
. В этом случае пишут 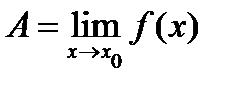 .
.
Если соответствующее неравенство в определении предела выполнено только для всех 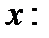
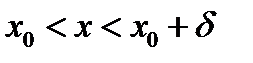 или для всех
или для всех 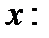
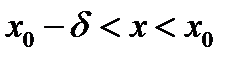 , то говорят, что существует односторонний предел функции
, то говорят, что существует односторонний предел функции 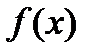 в точке
в точке 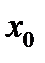 (
(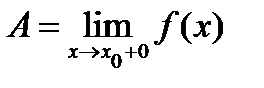 или
или 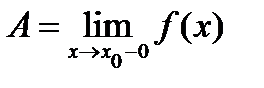 соответственно).
соответственно).
Определение 2. Число 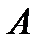 называется пределом функции
называется пределом функции 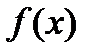 при
при 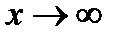 , если для любого
, если для любого 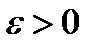 найдется такое число
найдется такое число 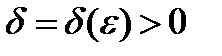 , что при
, что при 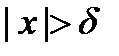 выполнено неравенство
выполнено неравенство 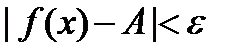 .
.
Если неравенство 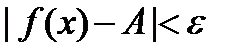 выполнено только для всех положительных или всех отрицательных значений аргумента
выполнено только для всех положительных или всех отрицательных значений аргумента 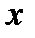 , говорят об одностороннем пределе при
, говорят об одностороннем пределе при 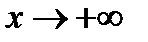 или при
или при 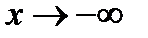 .
.
Функция 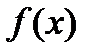 называется непрерывной в точке
называется непрерывной в точке 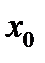 , если
, если 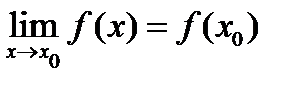 . Как правило, любая композиция элементарных функций (типа
. Как правило, любая композиция элементарных функций (типа 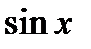 ,
, 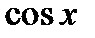 ,
, 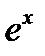 ,
, 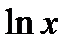 ,
, 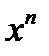 ,
, 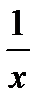 ) является непрерывной в любой точке определения. Поэтому вычисление предела таких функций в произвольной точке
) является непрерывной в любой точке определения. Поэтому вычисление предела таких функций в произвольной точке 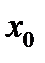 сводится к вычислению значения функции в этой точке. Если, однако, функция
сводится к вычислению значения функции в этой точке. Если, однако, функция 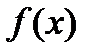 не определена в точке предела, этот прием не сработает. В таком случае говорят о наличии неопределенности в точке
не определена в точке предела, этот прием не сработает. В таком случае говорят о наличии неопределенности в точке 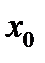 . Есть несколько стандартных типов неопределенностей и приемов вычисления предела (раскрытия неопределенности) в этих случаях.
. Есть несколько стандартных типов неопределенностей и приемов вычисления предела (раскрытия неопределенности) в этих случаях.
Пределы алгебраических функций на бесконечности.
Задача 2.1.а. Вычислить
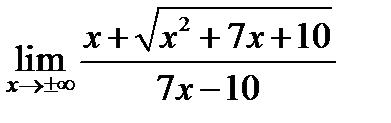
Решение. Старшая степень 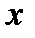 в числителе и знаменателе данной дроби равна 1. Поделим числитель и знаменатель одновременно на
в числителе и знаменателе данной дроби равна 1. Поделим числитель и знаменатель одновременно на 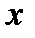 . Результат деления зависит от знака
. Результат деления зависит от знака 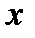 . Если
. Если 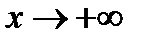 , то тогда получаем:
, то тогда получаем:
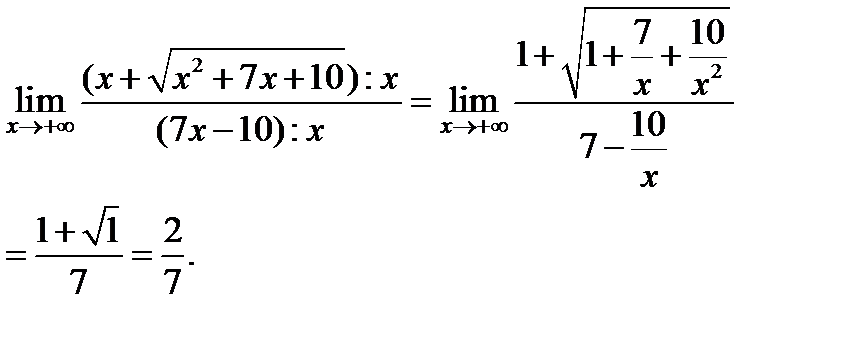
При 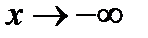 получаем:
получаем:
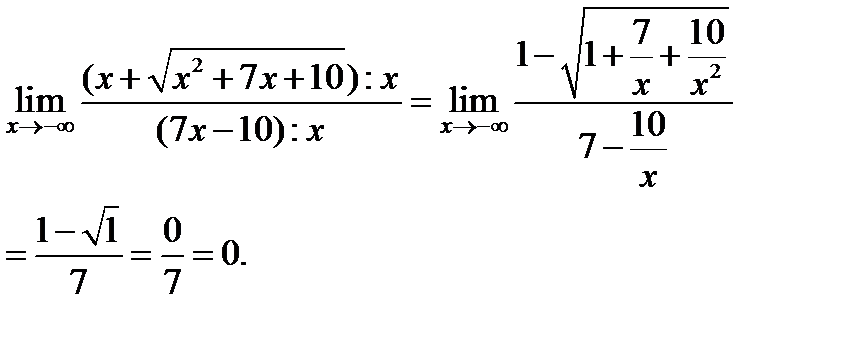
Здесь использовано очевидное соотношение 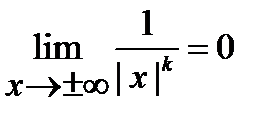 при любом
при любом 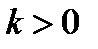 , и формула
, и формула 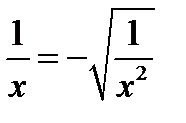 , справедливая при
, справедливая при 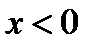 .
.
 2015-03-20
2015-03-20 432
432







