1. Дискретные случайные величины.
Пусть Х – дискретная СВ, которая приняла значения 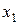 ,
, 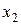 , …,
, …, 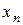 в результате п испытаний. Пусть известен закон распределения СВ Х, но неизвестен определяющий его параметр
в результате п испытаний. Пусть известен закон распределения СВ Х, но неизвестен определяющий его параметр 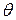 . Требуется найти точечную оценку этого параметра.
. Требуется найти точечную оценку этого параметра.
Обозначим вероятность того, что в результате испытания величина Х примет значение 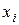 , через
, через 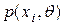 .
.
· Функция аргумента 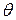 :
: 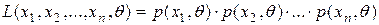 , где
, где 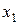 ,
, 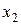 , …,
, …, 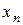 – фиксированные числа, называется функциейправдоподобиядискретнойслучайнойвеличины Х.
– фиксированные числа, называется функциейправдоподобиядискретнойслучайнойвеличины Х.
В качестве точечной оценки параметра 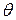 принимается значение
принимается значение 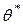 , при котором функция
, при котором функция 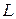 достигает максимума. Такую оценку
достигает максимума. Такую оценку 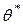 называют оценкойнаибольшегоправдоподобия.
называют оценкойнаибольшегоправдоподобия.
· Функцию 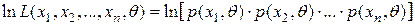 , называют логарифмической функцией правдоподобия.
, называют логарифмической функцией правдоподобия.
Точка максимума у обеих функций одна и та же, но вместо функции 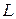 , удобнее анализировать функцию
, удобнее анализировать функцию 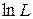 .
.
 2015-03-20
2015-03-20 348
348








