Пусть должно произойти n независимых опытов.
Обозначим 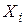 значение, которое примет СВ
значение, которое примет СВ 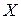 в i –ом опыте.
в i –ом опыте. 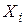 также будет являться СВ, имеющей тот же закон распределения, что и сама СВ
также будет являться СВ, имеющей тот же закон распределения, что и сама СВ 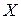 .
.
Пусть по результатам n опытов необходимо определить (приближённо) некоторый параметр 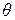 , связанный с законом распределения СВ
, связанный с законом распределения СВ 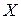 генеральной совокупности.
генеральной совокупности.
Приближённое значение параметра 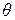 назовём его оценкой
назовём его оценкой 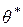 .
.
Любая оценка, вычисляемая на основе выборки, есть функция СВ 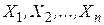 , и, значит, сама является случайной величиной. Если число наблюдений (опытов) сравнительно невелико, то замена неизвестного параметра
, и, значит, сама является случайной величиной. Если число наблюдений (опытов) сравнительно невелико, то замена неизвестного параметра 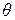 его оценкой
его оценкой 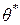 , например, математического ожидания выборочным средним, приводит к ошибке. Эта ошибка в среднем тем больше, чем меньше число опытов.
, например, математического ожидания выборочным средним, приводит к ошибке. Эта ошибка в среднем тем больше, чем меньше число опытов.
Для того, чтобы оценка неизвестного параметра давала хорошее приближение, она должна удовлетворять следующим требованиям:
1. Несмещённость.
2. Состоятельность.
3. Эффективность.
· Оценка называется несмещённой, если математическое ожидание оценки параметра по всевозможным выборкам данного объёма равно истинному значению определяемого параметра: 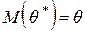 .
.
· Оценка называется состоятельной, если при увеличении объёма выборки оценка сходится по вероятности к истинному значению параметра:
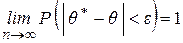 или
или 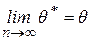 ,
,
где 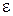 – сколь угодно малое положительное число.
– сколь угодно малое положительное число.
Из неравенства Чебышева следует, что для удовлетворения этого требования достаточно, чтобы оценка была несмещённой и 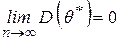 .
.
· Оценка называется эффективной, если 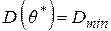 .
.
 2015-03-20
2015-03-20 654
654








