Непрерывные случайные величины

Пусть Х – непрерывная СВ, которая приняла значения 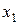, , 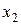…, 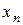в результате п испытаний. Пусть известна функция распределения плотности 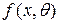, но неизвестен определяющий её параметр 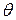. Требуется найти точечную оценку этого параметра.

· Функция аргумента 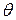: 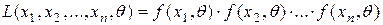, где 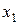, , 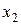…, 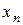– фиксированные числа, называется функцией правдоподобия непрерывной случайной величиныХ.

Метод оценки наибольшего правдоподобия неизвестного параметра 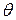такой же, как и в предыдущем случае – поиск точки максимума функции L.

Если в известной функции распределения 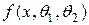неизвестны два параметра, то функция правдоподобия имеет вид

,

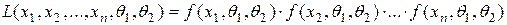и тогда необходимо найти точку максимума функции двух переменных.

Соответствующие логарифмические функции наибольшего правдоподобия вводятся так же, как и в случае дискретной случайной величины.